A gyakorlat témája: Összetett görbék kezelése, ívhossz- és területszámítás az Excel rendszerben.

A gyakorlat folyamán kiszámítjuk és ábrázoljuk egy parabolaívből és egy nyeregtetőből összetett lefedésű épület véghomlokzatának az alábbi ábrán vastag lila vonallal feltüntetett kontúrvonalát, továbbá meghatározzuk a végfal és a tető csatlakozási vonalának ívhosszát valamint a végfal területét. (Ezekre az adatokra pl. az épület kitűzéséhez, ill. a költségvetésben a szegélybádogozás és a vakolat mennyiségének kiírásához van szükség.) 

A megoldás alapgondolata az, hogy a tető és a végfal csatlakozási görbéjét (és ezzel összhangban magát a végfalat is) kis részekre, szakaszokra osztjuk, az egyes szakaszokon a görbét a megfelelő húrral helyettesítjük, és mind a görbe felrajzolását, mind pedig a terület és ívhossz kiszámításását ezen közelítés alapján végezzük el.

Az ábra mutatja a bekottázott véghomlokzatot és feltünteti a parabola és a nyeregtető-idom matematikai egyenletét is. A keresett felső kontúrgörbe magassági koordinátáját esetünkben úgy kapjuk meg, hogy az ugyanazon x értékhez tartozó yp parabola ill. yny nyeregtető magassági koordináták közöl mindig a nagyobbat vesszük.

Az ábra jobb felén jeleztük a felosztást is. Az l= 8.0 m-es fél fesztávolságot kiindulásul 10 egyenlő részre osztottuk, így egy-egy osztásköz 0.8 m. A görbe felrajzolása úgy történik, hogy x irányban végighaladunk – l -től +l -ig a teljes fesztávolság mentén és l/10 m-enként kiszámítjuk a magassági koordinátákat. Ezek alapján – mint látni fogjuk – az Excel rendszerben már el tudjuk készíteni az ábrát. De ugyanezeknek a koordináta-értékeknek a felhasználásával megoldható az ívhossz és a terület közelítő kiszámítása is. Az ábrán vastag vonallal van körülkeretezve egy, szomszédos osztáspontok (az xe és az xk) közötti elemi szakasz, ahol is már ki vannak számítva az ye és az yk magassági koordináták. Ha két szomszédos osztáspont között a görbét a megfelelő húrral közelítjük, akkor e húr dív hossza annak a derékszögû háromszögnek az átfogója lesz, amelynek(az ábrán szaggatott vonallal jelölt) vízszintes befogója a két x koordináta, függőleges befogója pedig a két y koordináta különbsége:

.

A végfalnak a vizsgált szakasz feletti elemi területsávját – ha a két szomszédos osztáspont között a görbét a megfelelő húrral közelítjük – egy trapéznak tekinthetjük, s így a szakaszhoz tartozó elemi területrész

.

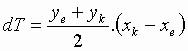Ha ezeket az elemi területeket ill. ívhosszakat minden szakaszra vonatkozóan kiszámítjuk és valamennyi szakszra nézve összegezzük, akkor a teljes ívhossz ill. a teljes terület mûszaki szempontból kielégítő pontosságú közelítését kapjuk.

A szükséges számításokat a mellékelt Excel táblázatban valósíthatjuk meg.

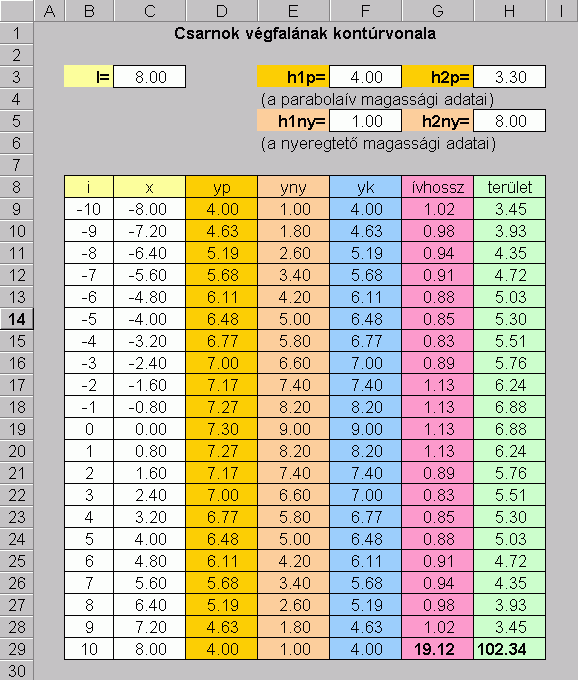
Először a bemenő paramétereket írjuk fel az ábrán látható módon, majd az értéket tartalmazó cellákat a Insert/Name/Define paranccsal nevezzük el (automatikusan a cella melletti szöveget ajánlja fel névnek a program, amelyet vagy elfogadjuk, vagy átírjuk), illetve közvetlenül beírhatjuk az aktuális cellacímet kijelző mezőbe. Ezután e neveken hivatkozhatunk a bemenő paraméterekre. Kezdetnek elég a kiinduló számértékeket elhelyezni az ábrán látható cellákba, a formázásokat későbbre hagyhatjuk.

A munka lényege a számítási oszlopok kitöltése. A B oszlopban el kell helyeznünk a csomóponti sorszámokat –10 től +10-ig, egyesével. Írjuk be az első két adatot (-10-et illetve -9-et, majd jelöljük ki két cellát együtt, s a jobb alsó sarkát „megragadva „húzzuk le” a kívánt (10) értékig. Jelöljük ki az B9:B29 tartományt és nevezzük el i-nek. A szakaszhatár pontok x koordinátái kerülnek a C oszlopba. Ezeket úgy számíthatjuk, hogy a sorszámmal megszorozzuk a Dx-et , azaz =i*l /10, majd másoljuk le akár a már gyakorolt Copy/Paste utasításpárral, akár az C9 –re klikkelve és a bal alsó sarkánál fogva „lehúzva” a megfelelő helyekre. Jelöljük ki az C9:C29 tartományt és nevezzük el x-nek. Az yp, yny és yk oszlopokban csak a 9. sorba kell képleteket beírni, s e képletek egyszerûen a címoldali ábrán a szokásos matematikai alakban megadott képletek Excel megfelelői:

Hasonlítsuk össze azzal, amikor nem definiálunk paraméterneveket:

Láthatjuk, hogy az x független változó helyébe az C oszlop x értékét tartalmazó cellája kerül. Itt a sor számjele előtt nem állhat $, mivel olyan változóról van szó, amelyet minden sorban más-más értékkel kell figyelembe venni, amikor a képleteket majd levisszük az alsóbb sorokba. A x hellyel nem változó konstans adatoknál viszont kötelező a $ legalább is a sor számjele előtt (az oszlopra utaló betü elött esetünkben mindegy, hogy teszünk-e $ jelet, vagy sem, mivel a képleteket csak saját oszlopukban másoljuk). Mindezt elkerülhetjük, ha elnevezzük a cellákat. Az ívhossz és terület oszlopaiba szintén csak a 9. sor képleteit kell beírni, s e képletek is az előző oldalon dív-re és dT-re a szokásos matematikai alakban megadott képletek Excel „fordításai”:

A képletek beírása során figyeljük meg, hogy a hatványozás jele a ^ jel, amely azonban bizonyos beállításoknál csak akkor jelenik meg, ha utána a hatványkitevőt (esetünkben ez 2) is beírtuk. A gyökvonásnak az SQRT() függvény felel meg. Ezt (angol Excel esetén) beírhatjuk a billentyûzetről, vagy megkereshetjük az Insert/Function… utasítással. Ez utóbbi különösen akkor hasznos ha nem tudjuk valamely használni kívánt függvény pontos megnevezését az éppen használt (pl. magyar nyelvû) Excel változatban, illetve nem tudjuk, milyen paramétereket kell megadni a függvény számára. A 9. sor kitöltése után a C9 … H9 cellákat (a jobb alsó sarkuknál fogva) levihetjük a szükséges sorokba. Ügyeljünk arra hogy az G és H oszlopokban eggyel kevesebb elemi ívhossz és terület szerepelhet, mint ahány koordináta érték van az C … F oszlopokban, hiszen a közök száma mindig eggyel kisebb az azokat határoló pontokénál. Az így üresen maradó G29 és H29 cellákban számoljuk ki az ívhossz és a terület közelítő értékét a részhosszak és területek összegeként. Klikkeljünk mondjuk az G29 cellába, majd az Excel munkalapunk felső „eszközsorában” (toolbar) kőzéptájon található S (AutoSum) jelre, és befejezésül üssük le az Enter billentyût. Ekkor megjelenik a közelítő ívhossz, ugyanezt az H29-cel megismételve pedig a közelítő terület.

Az ábrázolás (chart) elkészítése. Kitûzött feladatunkból még adósak vagyunk a végfal ábrázolásával. Annak érdekében, hogy ne csak a véghomlokzat felső határgörbéje jelenjen meg az ábrán, hanem a teljes zárt kontúrvonal, egészítsük ki kézi billentyûzéssel az x és az yk értékek oszlopait a következő oldali ábrán a lila keretben bemutatott három ponttal. Ezek rendre a jobboldali függőleges határvonal, az alapvonal és a baloldali függőleges oldalvonal megrajzolásához szükséges koordináták.

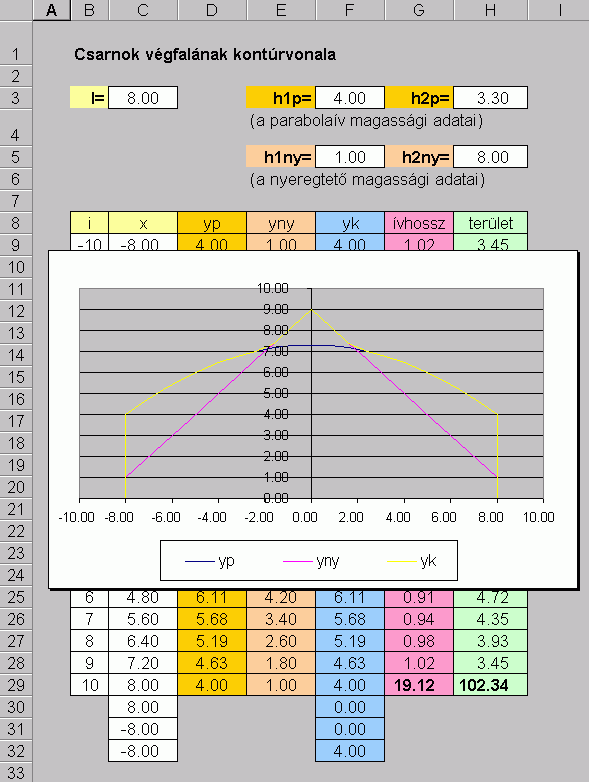
Magát az ábrát az Excel „Chart” utasításával készítjük el. A felső eszközsorban (toolbar) jobbról a 4. ikon a „Chart Wizard” a „diagram varázsló”. Erre klikkelve először is ki kell választanunk, hogy milyen jellegû ábrát akarunk. A koordinátákkal megadott alakzatok kirajzoltatására az XY Scatter a legalkalmasabb, tehát jelöljuk ki a listából ezt, és a megjelenő minták közül válasszuk a jobb alsót, a síma egyenesszakaszokkal való ábrázolást. A Next (következõ) „gomb”-ra klikkelve adhatjuk meg a Series „fül”-lel azokat a számsorozatokat, amelyeket ábrázolni akarunk. Ezek listája a megnyíláskor üres, az Add (adj hozzá) gombra klikkelve kell az ábrázolni kívánt x, és y értékek sorát megadnunk. Ehhez klikkeljünk először is a Name: mező jobb szélén levő nyomógombra, klikkeljünk a táblázatunk fejlécén a D8-as (yp) cellára, majd az X Values: jobb szélén levő nyomógombra, az egérrel a C9:C32 cellákon végighúzva adjuk meg az x értékeket. Ugyanígy az Y Values utáni mezőt is jelöljük ki, ide írjuk be az yp értékek megfelelő sorozatát: D9:D32 , majd az Add gomb lenyomásával a további x,yp illetve x,yk értékpárokat is adjuk meg. Ha ezeket megadtuk, a Next gombbal továbbléphetünk.

Ezzel tulajdonképpen végeztünk is a az ábrázolás előkészítésével, megjelenik az előzetes ábra, választhatunk, hogy az eredeti táblázatunkba objektumként vagy pedig egy új lapra kerüljön az ábra. A Finish-sel pedig beépül választás szerinti munkalapra. Ha objektumként szúrtuk be az ábrát, azt azután az egérrel mozgathatjuk skálázhatjuk, akár a táblázatok tetejére is vihetjük (ez a táblázatok mûködését semmiben nem zavarja). A Chart-ok formázására az Excel rendkívül változatos lehetőségeket nyújt. Ha egy Chart kerületére klikkelve kiválasztjuk azt, a főmenüben megjelenik a Chart tétel, ami lehetőségeket ad egy meglévő diagramm átszerkesztésére. A meglévő ábra egyes elemeire, pl egy diagrammvonalra duplaklikkelve, azt külön is formázhatjuk. Mindezen lehetőségek részletes és teljes leírása nem csak igen terjedelmes lenne, hanem értelmetlen is, hiszen a legfontosabb, amit e tárgyban magunkban kifejleszthetünk, az a felhasználóbarát rendszerek kezeléséhez szükséges „informatikai kultúra”. Tehát kisérletezzenek és alakítsák kedvükre az elkészített ábrát!