Számítógépek alkalmazása 2 - A CAD
alapjai (AutoCAD 2000)
2000/2001. év - II. félév
4.
gyakorlat
|
Ha kérdésed
van, ide írhatsz. Visszatérés az első lapra.
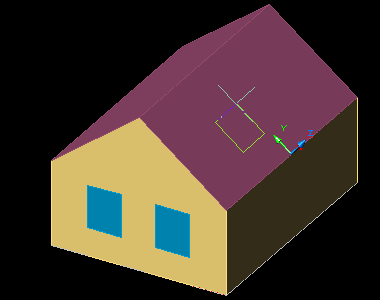
A feladat az alábbi ábrán
látható házszerű test térbeli (felület)modelljének
elkészítése:
(a 2000. évi országos gyermekrajz-pályázat 3-4 éves
korosztályának megosztott 2. díjas terve)
 |
• Hogy ismerős terepről
induljunk, legyen a ház alaprajza azonos a berendezési
gyakorlaton fölrajzolttal: azaz belmérete legyen 720×540cm,
falvastagsága 38cm. Ha még megvan,
akár folytatható is a múltkori rajz – persze az sem
veszít sokat, aki "újraszerkeszti" a 796×616 cm-es
befoglaló-téglalapot...
|
| •
3D nézetek A térbeli
rajzolásnak ugyan nem feltétele hogy lássuk is, mit
csinálunk – de általános tapasztalat szerint sokat
javít a rajzolás sebességén és minőségén.
Úgyhogy első lépésként mi is váltsunk inkább egy
térbeli nézetre. Ennek (mint lassan már megszokhattuk)
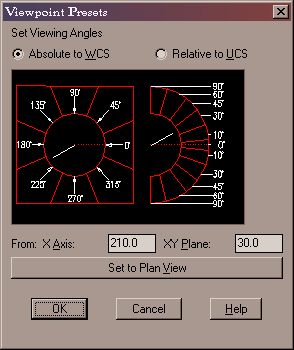
számos módja van: például a View •
3D Views • Viewpoint Presets menüpont (=VP
(alias ddVPoint) parancs). Ennek párbeszédpaneljén
megadhatjuk a nézési iránynak a vízszintes
alap-síkban, ill. attól mért szögét. E megadás
történhet a szögek megfelelő rovatba írásával –
vagy egyszerűen a megfelelő helyre való kattintással.
Népszerű, (és gyors) nézetbeállítási forma a 3dorbit
( View
• 3D Orbit) parancs használata. Ennek
egyetlen hátránya, hogy (az általunk használt,
2000-es verzióban) szinte lehetetlen a Z
tengelyt függőlegesben tartani. Lehet, hogy
konzervatizmusnak tűnik ilyen apróságon fönnakadni,
de (a gravitácó tiszteletén kívül) szerintem
meggyőző okok hozhatók, miért is jó, ha a
függőleges vonalak annak is látszanak: pl. a monitor
pixeles felépítéséből adódóan a függőlegestől
csak kismértékben eltérő vonalakon kis
"szakadások" jelennek meg – ez
figyelmeztethet pl. szerkesztési hibára, ha egy
függőlegesnek szánt vonal mégsem lenne az. View
• 3D Orbit) parancs használata. Ennek
egyetlen hátránya, hogy (az általunk használt,
2000-es verzióban) szinte lehetetlen a Z
tengelyt függőlegesben tartani. Lehet, hogy
konzervatizmusnak tűnik ilyen apróságon fönnakadni,
de (a gravitácó tiszteletén kívül) szerintem
meggyőző okok hozhatók, miért is jó, ha a
függőleges vonalak annak is látszanak: pl. a monitor
pixeles felépítéséből adódóan a függőlegestől
csak kismértékben eltérő vonalakon kis
"szakadások" jelennek meg – ez
figyelmeztethet pl. szerkesztési hibára, ha egy
függőlegesnek szánt vonal mégsem lenne az.
Még kevésbé javaslom az izometrikus nézetek
használatát (pl.  View •
3D Views • SW Isometric), ezek ugyanis
gyakran eredményeznek egymást takaró vonalakat, s
ezáltal sokszor megnehezítik a pont-kijelölést. (Még
rosszabb a helyzet az alaprajzilag 45°-os vonalakkal –
ezek lejtése ugyanis teljesen rejtve marad.) View •
3D Views • SW Isometric), ezek ugyanis
gyakran eredményeznek egymást takaró vonalakat, s
ezáltal sokszor megnehezítik a pont-kijelölést. (Még
rosszabb a helyzet az alaprajzilag 45°-os vonalakkal –
ezek lejtése ugyanis teljesen rejtve marad.)
|
 |
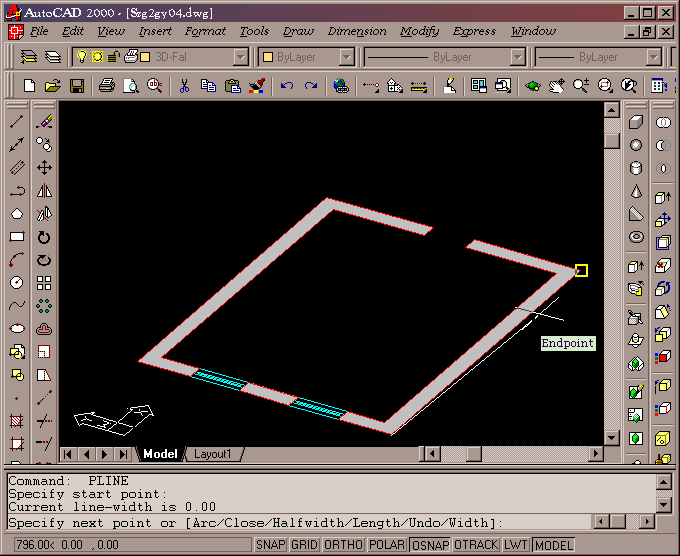
Az alábbi ábrán látható a kiindulási helyzet: a
beállított 3D nézetben is az eddig megszokott módon, a már
megrajzolt rajzelemek jellemző pontjainak felhasználásával (OSNAP) rajzolhatunk. A 3D rajzoláshoz
érdemes persze külön fóliá(ka)t létrehozni (és a
fölösleges 2D-s fóliákat lefagyasztani:  ).
).
| •
Térbeli 2D-s rajzelemek A
síkbeli elemek is térbelivé tehetők ha azokhoz
"vastagságot" (Thickness) rendelünk.
Ehhez – a rajzelem(ek) kijelölése után – a Modify
• Properties menü panelének Thickness
rovatában javítsuk ki az eddigi 0-át 300-ra. Ezek után a
vonalak, mint az alapsíkon álló "szalagok"
jelennek meg.
Egy zárt Pline kiemelésével
létrejött elem tehát még nem test, és erről meg is
győződhetünk, ha a View • Shade • Flat
Shaded, Edges On menüponttal
"árnyalt" képet kérünk a rajzról (l.
ábra). De ez nem általános szabály, mert pl. a
körnek magasságot adva, egy "tömör" hengert
kapunk, azaz (legalábbis a takartvonalas képen) nem
látunk a belsejébe.
Az ilyen "térbeliesített" 2D-s elemek
használatának mindenestere erős korlátja, hogy
magasságuk (nyilvánvalóan) minden végpontjukban
azonos kell maradjon.
|
 |
Megjegyzés: a
következőkben is a talán egyszerűbben értelmezhető árnyalt
képek mutatják a szerkesztés menetét – de ez persze nem
jelenti, hogy ez a szokásos megjelenítési mód! Ellenőrzési
célokra persze jó, és ilyen egyszerű szerkesztési
feladatoknál is megfelel, de komolyabb munkánál jellemzően a
"drótvázas" megjelenítést használjuk.
| •
3D rajzelemek A valódi 3D
rajzelemek közül a legegyszerűbb felület a 3dFace
(3dLap): egy (max. 4 oldalú) térbeli
négyszög. (A legegyszerűbb 3D elem a Line).
A 3D rajzelemekre nem vonatkoznak az előbb látott
korlátozások. Ez egyszerűen szemléltethető a tető
megrajzolásával, megmutatva egyúttal, hogy az XY
síkkal nem párhuzamos felületet is lehet szerkeszteni:
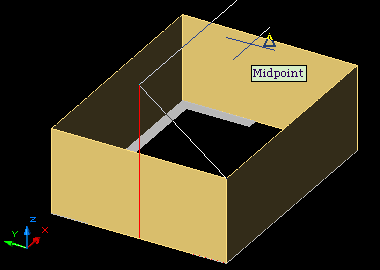
• A 3dFace első két pontját
megadhatjuk egyszerűen a meglévő "fal"
fölső élének végpontjaira kattintva. A harmadik, és
negyedik pont megadásánál használhatjuk a
pont-szűrőket (Point Filters): így módunk
van ugyanis arra, hogy egy pont (az ábrán épp a gerinc
túlsó végpontja) megadását kétfelé bontsuk. Mivel
tudjuk, hogy a pontnak a fal felezőpontja felett kell
lennie, írjuk be: .xy[Enter],
(gépelésből felmentetteknek: Shift +
jobb egérgomb, majd a gyorsmenüben: Point
Filters • .XY). Ezzel elértük, hogy elég
egy olyan pontot megmutatnunk, melynek x,
és y koordinátái megegyeznek
az általunk megadni kívánt pontéval. Erre
tökéletesen megfelel az ábrán is látható
felezőpont. Persze a z
koordináta megadására nem felmentést, csak haladékot
kaptunk; a felezőpont megadása után a program azonnal
számonkéri rajtunk tartozásunkat ((need Z):), ám mi
felkészülten vájuk a pillanatot, és beírjuk: 540[Enter]. Ez
lesz ugyanis a gerincmagasság (abszolút
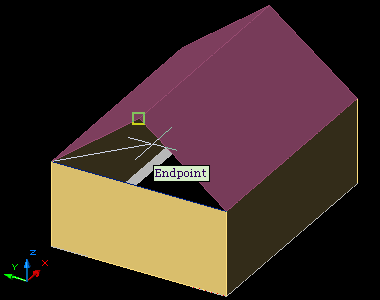
koordináta!). A másik tetősíkot előállíthatjuk a
már megrajzolt sík gerinc-vonalra való
tükrözésével .
|
 |
 |
Az oromfal megrajzolása
előtt térjünk vissza a 3D-Fal
fóliára (mert ugye a tetőt mindenki külön
fólián alkotta meg...). Itt egy újabb, 2D-s
rajzelemek számára elérhetetlen dolgot viszünk
véghez: változó magasságú rajzelemet rajzolunk!
Méghozzá (a meglévő végpontok megfogásával)
könnyedén: mindössze annyi a dolgunk, hogy a 3dFace
negyedik végpontjának megadása helyett Enter-t
ütünk. Azért nem minden fenékig papsajt! Az
árnyalt képen ugyan kevéssé látványos, de a
"normál", drótvázmodelles képen (View
• Shade • 2D Wireframe), és főleg
nyomtatásban zavaró lehet az alsó falrész és az
oromfal közötti vonal. Erre is van megoldás:
robbantsuk föl (Explode ) a téglalapot, és töröljük
ki az első és hátsó falakat (az oromfal marad!), majd
rajzoljunk helyettük ugyanolyan geometriájú 3dFace-eket
:o. ) a téglalapot, és töröljük
ki az első és hátsó falakat (az oromfal marad!), majd
rajzoljunk helyettük ugyanolyan geometriájú 3dFace-eket
:o.
Ezeknek ugyanis van egy utolsó trükk a tarsolyukban:
egyes éleik láthatatlanná tehetők! Ehhez csak el kell
indítanunk az Edge parancsot, és rá
kell mutatnunk a 3dFace-ek eltüntetni
kívánt éleire (a közös élekre elég egyszer), majd
Enter.
|
Megjegyzés: vannak persze
örök elégedetlenek, akiket még olyan apróságok is zavarnak,
mint pl. hogy most a végfal (lévén két darabból) csak
nehézkesen jelölhető ki, és ha árnyalásnál be vannak
kapcsolva az élek (...Edges on), még mindig látszik
a határvonal. Van azért megoldás: a PFace
rajzelem alkalmazása. Ez tulajdonképpen speciális
"összekapcsolt" 3DFace elemeket
jelent. Megadási módja nem igazán felhasználó-barát:
először meg kell adni az elem csúcspontjait, majd (Enter
után) az egy-egy lapot alkotó csúcsokat (több lap is
megadható). Ez azért konvex ötszög esétén nem jelent
megoldhatatlan nehézséget: sorban meg kell adni a lefedendő
terület öt csúcsát (Enter), majd az összekötendő
csúcsokat: 1 2 3
4 5[Enter]
(a lap lezárására) [Enter] (a Pface
lezárására).
• Felhasználói
koordináta-rendszerek (UCS)
| Az alsó ablakokat még
megrajzolhatjuk az alap-síkon egyszerű vonalként (amit
azután helyére emelünk (@0,0,100),
majd magasságot (150)
rendelünk hozzá). Viszont a tetőablakok megrajzolása
ebben a koordinátarendszerben már kissé nehézkes
lenne. Ilyen esetekre lett kitalálva a fehasználói
koordinátarendszer: UCS = User
Coordinate System – ez egyben a
koordináta-rendszerek módosítását/váltását
szolgáló parancs neve is. Ezt a "saját"
koordináta-rendszert oda, akkor, és úgy helyezzük el
és át, ahogy és amikor akarjuk. Legáltalánosabban
alkalmazható megadási mód a három-pontos módszer:
ekkor meg kell adnunk az új koordináta-rendszer
origójának helyét, egy második pontot az X
tengely pozitív felén, végül egy harmadikat, amely az
XY síkon, annak is pozitív y
tartományán van.
Ebben a koordináta-rendszerben legyen az ablak a
saroktól 240cm-re X,
100cm-re Y
irányban (Tracking!). Legtöbbször persze nem
ilyen egyszerű az ablak helyének megadása, hanem
alaprajzából, és/vagy (parapet)magasságából
(~vízszintes, ill. függőleges vetületéből) adódik!
|
 |
VÉGE!






