Számítógépek alkalmazása 2 - A CAD
alapjai (AutoCAD 2000)
2000/2001. év - II. félév
5.
gyakorlat
|
Ha kérdésed
van, ide írhatsz. Visszatérés az első lapra.
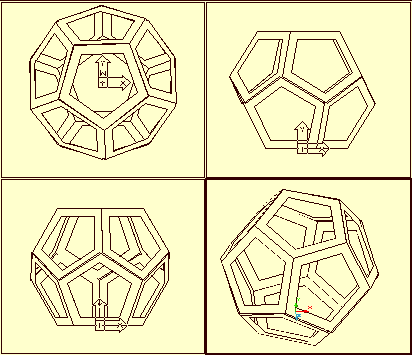
A feladat az alábbi ábrán
látható dodekaéder megrajzolása:
 |
•
2D SZERKESZTÉS • Az oldallap
egy 10 egység sugarú körbe írható ötszög, benne 8
egység sugarú körbe írható lyukkal. Az (első)
ötszöget legegyszerűbb a Polygon
paranccsal (vagy  ikonnal)
rajzolni: ekkor meg kell adnunk a középpontot (ez
legyen most az origó), azt hogy körbe, vagy kör köré
írt elemet akarunk rajzolni, s azt, hogy hány-oldalú
legyen a sokszög (5). ikonnal)
rajzolni: ekkor meg kell adnunk a középpontot (ez
legyen most az origó), azt hogy körbe, vagy kör köré
írt elemet akarunk rajzolni, s azt, hogy hány-oldalú
legyen a sokszög (5).
(Ha valaki nem akar idegen
"segítséget" igénybe venni, az
megrajzolhatja az ötszöget, mint PLine
elemet: 10<0 10<72 10<144 10<216 10<288,
Close... A végeredmény ugyanaz.)
A belső lyukat is hozzuk létre (pl. Offset
(táv: 2), majd az oldallap
kilyukasztásának előkészítéseként alakítsuk a (PLine)
vonalakat felületté a REGion
paranccsal.
|
Az így létrejött felületekre alkalmazhatók a Boolan-műveleletek:
két (vagy több) elem összeadható egymással (Union ), kivonható egymásból (Subtract
), kivonható egymásból (Subtract ), ill. közös részükből (részeikből)
új elem hozható létre (Intersect
), ill. közös részükből (részeikből)
új elem hozható létre (Intersect ). Mi most a kivonást fogjuk kipróbálni: ennek
egyetlen "nehézsége", hogy mivel több elemből több
elemet is kivonhatunk (így a kivonás előtt még akár két
összeadást is végezhetünk ugyanazzal a paranccsal), emiatt
nem elég egyszerűen megmutatni a két rajzelemet, hanem az
első elem kiválasztása után Enter-t kell nyomni, majd megadni
a kivonni szándékozott második elemet, végül újra Enter.
). Mi most a kivonást fogjuk kipróbálni: ennek
egyetlen "nehézsége", hogy mivel több elemből több
elemet is kivonhatunk (így a kivonás előtt még akár két
összeadást is végezhetünk ugyanazzal a paranccsal), emiatt
nem elég egyszerűen megmutatni a két rajzelemet, hanem az
első elem kiválasztása után Enter-t kell nyomni, majd megadni
a kivonni szándékozott második elemet, végül újra Enter.
| •
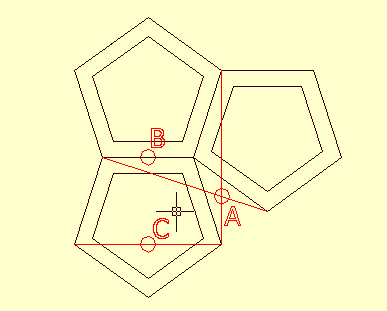
3D szerkesztés A mellékelt
ábrán látható módon tükrözzük kétszer az eredeti
ötszöget egy-egy oldalára.
A létrejött elemek föfoghatók a dodekaéder síkba
kiterített oldalainak. Ha vissza akarjuk őket
"hajtogatni" térbelivé, nyilván az előbb
tükrözésre használt közös él mentén forognának.
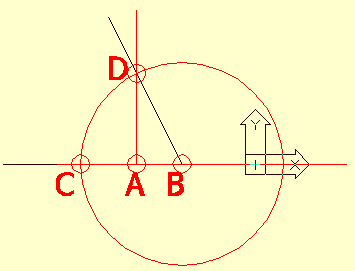
Ily módon a két lap fölhajtásakor a csúcsok
fölülnézetben az A ponton átmenő
két egyenesen mozognak, és akkor érik el végső
helyüket, ha (az A pont felett)
találkoznak.
Rajzoljunk A-ba egy függőlegest (Line,
végpont: A, majd @0,0,20).
Vegyünk föl egy olyan UCS-t, melynek
origója B pont, Z
tengelye pedig a két oldallap közös éle (pl. UCS
ZA...). E koordinátarenszerben
(természetesen axonometrikus nézetben) megrajzolható a
B pont köré írt kör, melyen a C
pont mozog. (A sugár megadásakor jól jöhet jól
jöhet a .xy szűrő, hiszen a sugár a BA
távolság vetülete lesz).
|
 |
 |
Mivel a legtöbb
szerkesztési parancs az aktuális koordinátarendszer
alap-síkjára vetítve működik, a Trim
paranccsal akkor is képes ki tudunk metszeni a körből,
ha az nincs egy síkban a "metsző" vonalakkal
(azaz az A-n átmenőY,
és Z irányú vonalakkal). A
megmaradó körív-darab mutatta szöggel forgassuk el a C
pontot tartalmazó ötszöget BC-BD szöggel (a másik
ötszög törölhető).
A többi négy alsó oldallap kiosztható az Array
paranccsal, majd az alsó fél-dodekaéder tükrözhető
térben (Mirror3d) a ferde lapok
felezőpontjai által megadott vízszintes síkra – és
máris létrejött a "papír"-dodekaéder.
|
Minden rajzelem "emlékszik", milyen volt
megrajzolásakor a Z irány (ami persze később
vele együtt forog): jelen esetben minden oldallap normálisa a
test belseje felé mutat. Ezt kihasználva az összes lap
egyetlen utasítással testté változtatható: az Extrude
parancsnak adjuk meg az összes (12) oldallap-elemet (all),
majd magasságként pl. 1.5-öt. A létrejövő
testekre is alkalmazhatók a Boolan-műveleletek: az
összadás (Union) művelettel egyetlen testté
egyesíthetjük a lapokat.
Megjegyzés: haladók
megpróbálhatják módosítani a fönti szerkesztést úgy, hogy
a test belső élei ne legyenek "leharapva", azaz az
éleknek deltoid metszete legyen!
VÉGE!


