BME Építészmérnöki Kar, Építészeti Ábrázolás Tanszék
tanszékvezető: Dr. Szoboszlai Mihály

CAAD és építészinformatika (BMEEPAG0202)

Parametrikus modellezés (GDL)

Kiss Zsolt
egyetemi adjunktus


2. gyakorlat

Geometriai transzformációk, ciklusok

2002. febr. 21. 13:43:37

Készítsünk el egy, az ábrán látható egyszerű csigalépcsőt!

(egyenlőre szerkezet nélkül)

Változtatható legyen az
  • emeletmagasság,
  • az orsótér sugara,
  • a kar szélessége,
  • a lap vastagsága,
  • a fellépés legnagyobb értéke
  • a '2m + sz' értéke
  • a lépcsőfok anyaga
A járóvonalat vegyük fel a kar szélességének 2/3 részénél (a belső oldalról)
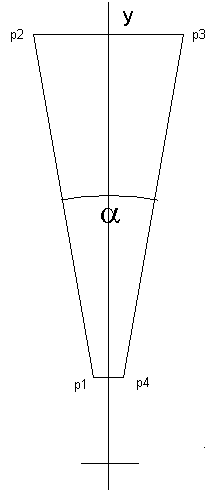
Az alapelem egy trapéz alakú lépcsőfok, melyet az y tengelyre szimmetrikusan 'írunk' le. A belépésszélességet a járóvonalon számítjuk ki, az egyszerűség kedvéért ívesen.

ívhossz = sugár * nyílásszög*
* radiánban

Így kiszámíthatjuk a fok "nyílásszögét", a-t, amelyből aztán a koordinátákat.
Célszerű kiszámítani az egységnyi sugárhoz tartozó x és y értékeket, hogy a cikluson belül nem kelljen újra és újra szögfüggvénnyekel számolni.
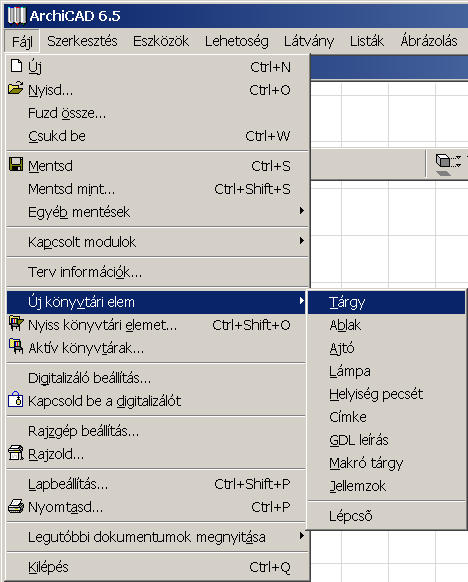
Hozzunk létre egy új könyvtári elemet a
File/Új könyvtári elem/Tárgy
menüponttal.

Definiáljuk a szükséges paramétereket a Paraméterek ablakban
és adjuk meg rögtön a kezdeti értékeket is. 

e       emeletmagasság                      3.00 (m)
b_kar   karszélesség                        1.20 (m)
r_orso  orsótér sugara                      0.30 (m)
v       a lépcsőfok vastagsága              0.06 (m)
sz2m    a '2m + sz' értéke                  0.63 (m)
mmax    maximális fellépésmagasság          0.18 (m)
mat     a lépcsőfok anyaga                  11

A Vezérleírásba írjuk be azokat a számításokat, melyek eredményeit mind a 2D leírásban, mind a 3D leírásban használni fogunk
csigalepcso / Vezérleírás 

n=CEIL (e/mmax)
m=e/n
sz=sz2m-2*m
alfa=sz/(r_orso+b_kar*2/3)/PI*180
x=SIN(alfa/2)
y=COS(alfa/2)


fellépések száma 
fellépések tényleges magassága
belépés szélessége
lépcsőfok nyílásszöge
egységnyi sugárhoz tartozó x
egységnyi sugárhoz tartozó y       
Így a cikluson belül nem kell
újra és újra szögfüggvénnyekel
számolni, ami lelassítaná a programot)

A 3D leírásban írjuk le az objektumot.
Egy hasábot (PRISM) forgatunk körbe, úgy, hogy közben fel is emeljük.
csigalepcso / 3D leírás 

MATERIAL mat
ADDZ m-v
FOR i=0 TO n-1
  PRISM 5,v,
    -r_orso*x, r_orso*y,
    -(r_orso+b_kar)*x, (r_orso+b_kar)*y,
     (r_orso+b_kar)*x, (r_orso+b_kar)*y,
     r_orso*x, r_orso*y,
     -r_orso*x, r_orso*y
  ROTZ alfa
  ADDZ m
NEXT i


globális anyag beállítása
az első lépcsőfok alja m-v magasságban
ciklus i nullától nő (n-1)-ig
a PRISM alappoligonja 5 pont ,v vastag,
x1, y1,
x2, y2,        
x3, y3,        
x4, y4,        
x5, y5,        
KR* elforgatása Z körül alfával
KR* felemelése Z mentén m-mel
ciklus vége
*KR : koordinátarendszer

A 2D leírásba írjuk le az objektum 2D-s nézetét.
Másoljuk le a 3D leírást töröljük ki a felesleges sorokat és javítsuk ki a pirossal jelölt részeket
csigalepcso / 2D leírás 

FOR i=0 TO n-1
  POLY2 5,1,
    -r_orso*x, r_orso*y,
    -(r_orso+b_kar)*x, (r_orso+b_kar)*y,
     (r_orso+b_kar)*x, (r_orso+b_kar)*y,
     r_orso*x, r_orso*y,
    -r_orso*x, r_orso*y
  ROT2 alfa
NEXT i


ciklus i nullától nő egyesével (n-1)-ig
POLY2 poligonja 5 pont ,1-es kitöltés,
x1, y1,
x2, y2,        
x3, y3,        
x4, y4,        
x5, y5,        
KR elforgatása alfa szöggel
ciklus vége

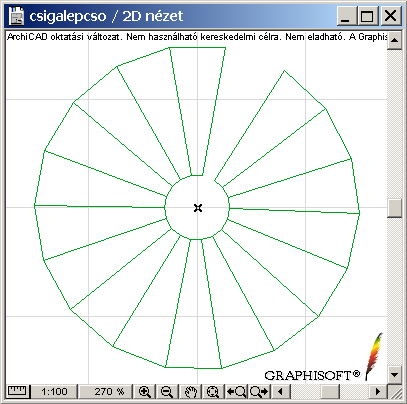
A 2D kép még nem igazán tökéletes, nincs járóvonal jelölve és nincs megoldva a kar "elmetszése".


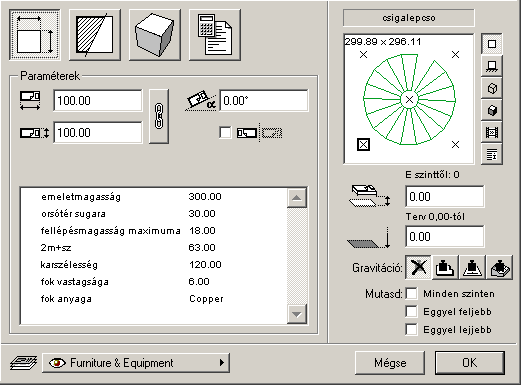
Módosítsuk a 3D leírást.
Tegyük ívessé a széleket! Ezt a CPRISM_ elemmel tehetjük meg.
csigalepcso / 3D leírás 

IF tomor THEN v=m
RESOL 72
ADDZ m-v
FOR i=0 TO n-1
  CPRISM_ mat,mat,mat,
   8,v,
   -r_orso*x, r_orso*y,15,
   -(r_orso+b_kar)*x, (r_orso+b_kar)*y,15,
     0,0,900,   
    (r_orso+b_kar)*x, (r_orso+b_kar)*y,3000+15,
     r_orso*x, r_orso*y,15,
     0,0,900,
     r_orso,alfa-oszlop*360,4000,      
    -r_orso*x, r_orso*y,1
  ROTZ alfa
  ADDZ m
NEXT i


Ha tömör a 'lépcső' legyen a v=m
A felbontás legyen a kör hetvenkettede
az első lépcsőfok alja m-v magasságban
ciklus i nullától nő (n-1)-ig
a CPRISM_ anyagai a tetején, alján, oldalán
alappoligonja 8 pont ,v vastag,
x1, y1,maszk1,
x2, y2,maszk2,
középpont x, y,         
x3, y3,maszk3,        
x4, y4,maszk4,
középpont x, y,         
sugár, alfa, maszk
x5, y5,maszk5
KR* elforgatása Z körül alfával
KR* felemelése Z mentén m-mel
ciklus vége
*KR : koordinátarendszer