| A 4. gyakorlat a lépcső alátámasztó szerkezetének modellezése
A lépcső gyámolítása lehet 1 vagy több gerendával, illetve teljes felületen
alátámasztva (pl.: vasbeton lemezlépcső)
Az alátámasztást a BPRISM_objektummal készítjük
A vázlat alapján meghatározzuk a gerenda kiterített modelljének koordinátáit.
Előállítjuk a gerendát a CPRISM_ objektummal (így tudjuk könnyen ellenőrizni), majd átalakítjuk BPRISM_ objektumra.
A szabályosan ismétlődő koordinátákat ciklusban állítjuk elő (hiszen nem tudjuk előre, hány darab lépcsőfokunk lesz) és egy un. verembe helyezzük.
|

|
Szükséges néhány új paraméter definiálása:
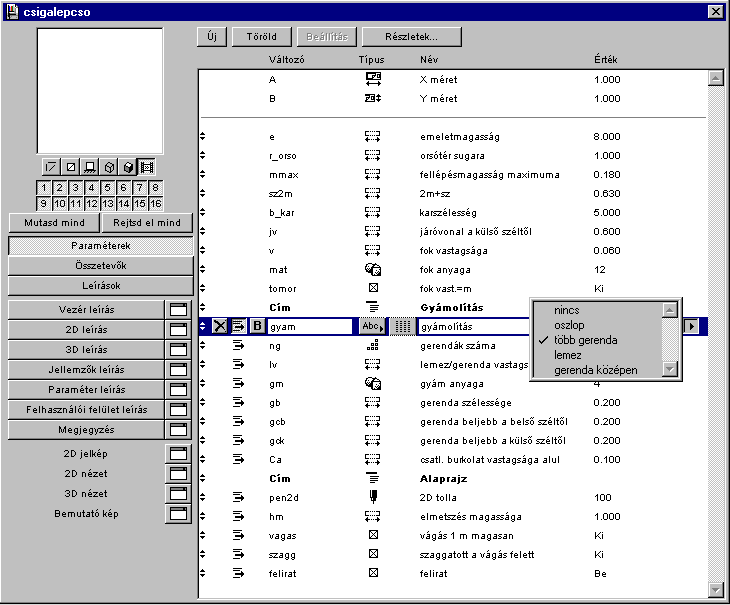
gyam: a gyámolítás módja, szöveg (string) típusú változó
Szükség van az alátámasztó gerendák számára (ng)
és a gerenda(ák) geometriai adataira (gb,lv,gcb, gck)
A ca a padlóvonal
és az alsó feltámaszkodási hely közötti magasságkülönbség
a Parameter Script-ben állítsuk be az előre definiált értékeket:
|
|
csigalepcso / Paraméterleírás
|
VALUES "gyam" "nincs",
"oszlop",
"több gerenda",
"lemez",
"gerenda középen"
VALUES "ng" RANGE [1,]
|
a gyámolítás lehet "csak járólapok",
"oszlop", (az orsótérben)
"több gerenda",
"lemez",
"gerenda középen"
A gerendák száma "ng" 1 vagy nagyobb
| |
Készítsük el először teljes felületen gyámolított lépcső 3D leírását
|

|
|
csigalepcso / 3D leírás
|
! csigalépcső 2.0
Kiss Zsolt
!-------------------------------
! lépcső járólapok
!-------------------------------
RESOL 72
IF gyam="oszlop" THEN
oszlop=1
v=m
ENDIF
IF tomor THEN v=m
ROTZ alfa/2
ADDZ m-v
FOR i=0 TO n-1
CPRISM_ mat,mat,mat,
8,v,
-r_orso*x, r_orso*y,15,
-(r_orso+b_kar)*x, (r_orso+b_kar)*y,15,
0,0,900,
(r_orso+b_kar)*x, (r_orso+b_kar)*y,3000+15,
r_orso*x, r_orso*y,15,
0,0,900,
r_orso,alfa-oszlop*360,4000,
-r_orso*x, r_orso*y,1
ROTZ alfa
ADDZ m
NEXT i
!--------------------------------------------
DEL TOP
szk = (r_orso+b_kar)*alfa/180*PI
beta = ATN(m/szk)
lvx = lv/SIN(beta)
lvy = lv/COS(beta)
FOR i=0 TO n-1
PUT i*szk, (i+1)*m-v,15
PUT (i+1)*szk, (i+1)*m-v,15
NEXT i
ROTZ 180
ADDY -r_orso-b_kar
ROTX 90
BPRISM_ gm,gm,gm,
5+2*n, -b_kar, r_orso+b_kar,
lvx+v/m*szk,0,15,
lvx+v/m*szk,-ca,15,
0,-ca,15,
GET (2 * n * 3),
n*szk,n*m-v-lvy,15,
lvx+v/m*szk,0,-1
|
A 3D Script eleje változatlan
A felbontás legyen a kör hetvenkettede
Ha tömör a 'lépcső' legyen a v=m
A lépcső induló éle az y tengelyen legyen
az első lépcsőfok alja m-v magasságban
ciklus i nullától nő (n-1)-ig
a CPRISM_ anyagai a tetején, alján, oldalán
alappoligonja 8 pont ,v vastag,
x1, y1,maszk1,
x2, y2,maszk2,
középpont x, y,
x3, y3,maszk3,
x4, y4,maszk4,
középpont x, y,
sugár, alfa, maszk,
x5, y5,maszk5,
KR* elforgatása Z körül alfával
KR* felemelése Z mentén m-mel
ciklus vége
*KR : koordinátarendszer
KR visszaállítása alaphelyzetbe
a külső íven mért belépés szélesség
az itt mért meredekség
a gerenda vízszintes metszete
a gerenda függőleges metszete
koordináták és a maszk értékek a verembe
a lépcső
a lépcsőtartó tengelyének eltolása a külső sugárral
a lépcsőtartó tengelyének függőlegesbe állítása
(y tengelyű hengerre simít a BPRISM_)
a BPRISM_ anyagai a tetején, alján, oldalán
alappoligon pontjainak száma ,'vastagság', sugár
x1, y1,maszk1,
x2, y2,maszk2,
x3, y3,maszk3,
2*n pont, 2*n*3 szám (x, y, maszk) a veremből,
..
..
|

|

|
|
Módosítsuk 3D leírást úgy, hogy tetszőleges számú gerendával lehessen alátámasztani a lépcsőt!
|
|
csigalepcso / 3D leírás
|
! csigalépcső 2.1
Kiss Zsolt
!-------------------------------
! lépcső járólapok
!-------------------------------
RESOL 72
IF gyam="oszlop" THEN
oszlop=1
v=m
ng=0
ENDIF
IF tomor THEN v=m
ROTZ alfa/2
ADDZ m-v
FOR i=0 TO n-1
CPRISM_ mat,mat,mat,
8,v,
-r_orso*x, r_orso*y,15,
-(r_orso+b_kar)*x, (r_orso+b_kar)*y,15,
0,0,900,
(r_orso+b_kar)*x, (r_orso+b_kar)*y,3000+15,
r_orso*x, r_orso*y,15,
0,0,900,
r_orso,alfa-oszlop*360,4000,
-r_orso*x, r_orso*y,1
ROTZ alfa
ADDZ m
NEXT i
!--------------------------------------------
IF gyam="nincs" THEN ng =1
IF gyam="lemez" THEN
gb=b_kar
gcb=0
gck=0
ng=1
ENDIF
IF gyam="gerenda középen" THEN
gcb=(b_kar-gb)/2
ng=1
ENDIF
IF ng > 0 THEN
IF ng > 1 THEN dr=(b_kar-gb-gcb-gck)/(ng-1)
r0=r_orso+gcb+gb
FOR j=0 TO ng-1
DEL TOP
r = r0 + j*dr
szk = -r*alfa/180*PI
beta = ATN(m/szk)
lvx= lv/SIN(beta)
lvy = lv/COS(beta)
FOR i=0 TO n-1
PUT i*szk, (i+1)*m-v,15
PUT (i+1)*szk, (i+1)*m-v,15
NEXT i
ROTZ 180
ADDY -r
ROTX 90
BPRISM_ gm,gm,gm,
5+2*n, -gb, r,
lvx+v/m*szk,0,15,
lvx+v/m*szk,-ca,15,
0,-ca,15,
GET (n*2*3),
n*szk,n*m-v-lvy,15,
lvx+v/m*szk,0,-1
NEXT j
ENDIF
|
A 3D Script eleje változatlan
A felbontás legyen a kör hetvenkettede
Ha tömör a 'lépcső' legyen a v=m
Forgassuk el KR-t úgy, hogy az induló él Y irányú legyen
az első lépcsőfok alja m-v magasságban
ciklus i nullától nő (n-1)-ig
a CPRISM_ anyagai a tetején, alján, oldalán
alappoligonja 8 pont ,v vastag,
x1, y1,maszk1,
x2, y2,maszk2,
középpont x, y,
x3, y3,maszk3,,
x4, y4,maszk4,
középpont x, y,
sugár, alfa, maszk,
x5, y5,maszk5
KR* elforgatása Z körül alfával
KR* felemelése Z mentén m-mel
ciklus vége
*KR : koordinátarendszer
dr: gerendák tengelytávolsága
az első gerenda külső ívének sugara
ciklus 0-tól (gerendák száma - 1)-ig
Összes koordináta-transzformáció törlése
az aktuális gerenda külső ívének sugara
az itt mért belépés szélesség
az itt mért meredekség
a gerenda vízszintes metszete
a gerenda függőleges metszete
ciklus 0-tól (lépcsőfokok száma-1)-ig
A verembe helyezem az i-edik lépcsőfok,
majd az i+1-edik lépcsőfok koordinátáját
5 egyedi pont + fokonként két pont
1. egyedi pont
2. egyedi pont
3. egyedi pont
A veremből kiolvasok fokonként két pontot
három-három értékével (x,y,maszk)
4. egyedi pont
Az 1. pont a bezárásához (maszk=-1)
|
|

