BME Építészmérnöki Kar, Építészeti Ábrázolás Tanszék.
CAAD és
Építészinformatika,VBA programozás (Excel, AutoCAD)
Előadó: dr. Peredy József prof. em.
A tárgy anyagának helye az építészmérnöki munkában.

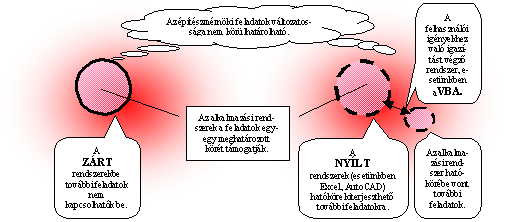
Az építészmérnöki munka ma már nélkülözhetetlen segítői a különböző számítógépes alkalmazói programrendszerek, különösen a CAAD (Computer Aided Architectural Design) rendszerek. Ezek munkánkat sokkal hatékonyabbá és kényelmesebbé teszik. Ugyanakkor minden lezárt rendszer szükségképpen csak a feladatok véges körére terjedhet ki, míg az építészmérnöki munka változatossága beláthatatlan. Ma már minden alkalmazói rendszer törekszik a nyitottságra, nevezetesen arra, hogy a felhasználó viszonylag könnyen hozzáigazíthassa a rendszert mindenkori feladatának igényeihez (angolul: customize), így mintegy kibővíthesse annak eredeti hatókörét. Kezdetben az egyes alkalmazói rendszerek egymástól függetlenül, egyedi megoldásokkal (makrók, szkriptek, speciális programnyelvek) igyekeztek ezt megvalósítani. Napjainkban kialakulni látszik egy egységesebb megoldás, a VBA rendszer (Visual Basic for Application – Szemléletes Basic az Alkalmazások számára). Ennek alapja a sokak véleménye szerint a nem főhivatásként programozó szakember számára "legbarátságosabb" programnyelv, a BASIC, ill. ennek egy korszerű, szemléletes változata. Ezt egészíti ki egy illesztő, amely lehetővé teszi az alkalmazási rendszereknek és a BASIC programoknak a hatékony együttdolgozását. A BASIC nyelvet Kemény János professzor (1926 – 1992) dolgozta ki az Egyesült Államokban. (Az arckép Kemény Jánost, mint a budapesti Berzsenyi gimnázium tanulóját ábrázolja.)
A tárgy keretében olyan építészmérnöki feladatokkal foglalkozunk, amelyekre az Excel és az AutoCAD rendszerek VBA programozási kiterjesztésével adhatunk célszerű megoldásokat. A VBA programozással való ismerkedést az Excel rendszer keretében kezdjük, mert ez makrók formájában "magától" képes egyszerű VBA programokat írni.
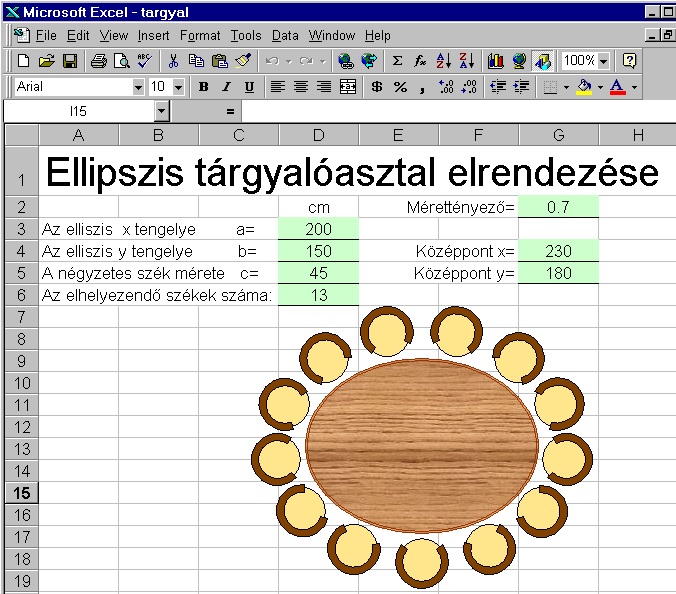
1. Feladat. Tárgyalóasztal alaprajzi elrendezése.

A feladat egy ellipszis alakú asztalból és a körülötte elhelyezkedő ülőhelyekből álló tárgyalóegység kialakítása. Ha ez egy irodaház tervezése során többször előforduló feladat, és/vagy az asztalméret ill. az ülőhelyszám tekintetében különböző változatokat akarunk kipróbálni, akkor mindenképpen célszerű a feladatot automatizálni, a programrendszerünk kész utasításkészletét ennek a feladatnak a megoldásával kiegészíteni. Megjegyzendő, hogy még egyedi esetben is igen nehézkes és tökéletlen az ülőhelyek ellipszis asztal körüli elrendezésének a "kézi" megoldása, ha csak a jelenleg használatos alkalmazási rendszerek alapszolgáltatásai állnak rendelkezésünkre.
1.1 Az
Kezdjük a munkát az asztal megrajzolásával. Nyissuk meg az Excel rendszert. A megjelenő munkalap (worksheet) alján látjuk a rajzolóeszközök sorát. (Ha nem lenne ott, akkor a
View/Toolbars/Drawing beklikkelésével hívható elő.) Az asztal alaprajzi jelölésére rajzojunk a lapon tetszőleges helyen és mérettel egy ellipszist, adjunk neki valamilyen tetszetős körvonalat és kitöltést. Ha néhány változat megrajzolása után elégedettek vagyunk az eredménnyel, készítessük el az Excellel az asztalrajzolás VBA programját.E célból klikkeljünk a
Tools/Macro/Record New Macro... utasításra, a megjelenő ablakba írjuk be az asztalrajzoló makró nevét, ha gondoljuk, beírhatunk még a "Shortcut key" mezőbe egy betűjelet is, aminek a Ctrl billentyűvel együtt történő leütésével majd az elkészült makrót "rövid úton" lefuttathatjuk, végül OK. Ez után gondosan rajzoljuk meg újra a megfelelőnek talált asztalalakot, s az Excel egyidejűleg feljegyzi a rajz "programját". A művelet befejeztével a Tools/Macro/Stop Recording utasításra (vagy a rajzmezőben automatikusan megjelenő azonos megnevezésű kis ideiglenes "gombra") klikkelve zárjuk le a makrót.Töröljük ki az asztal ábráját, és győződjünk meg a programunk működéséről a
Tools/Macro/ Macros... utasítással, a megjelenő ablakban kiválasztva a kívánt makrónevet, és Run. Az Excel által elkészített makrót, rövid programot, ugyanígy nézhetjük meg, a Run helyett Edit –et klikkelve. A program (az egyéni választástól függő – az alábbi programmintában kék színnel jelölt – méretektől, körvonaltípustól és kitöltéstől eltekintve) a következőképpen fog kinézni (megjegyzendő, hogy a vörös színnel írottak nem részei az Excel által a mi kézi munkánk nyomán automatikusan feljegyzett programnak, csak a megértést kívánják megkönnyíteni):Sub asztal()
'(1)'
(2)' Asztal Macro
(3)' Macro recorded 1/16/02 by jperedy
(4)'
(5)' Keyboard Shortcut: Ctrl+a
(6)'
(7)ActiveSheet.Shapes.AddShape(msoShapeOval,
157.8, 259.8, 133.2, 73.2).Select '(8)Selection.ShapeRange.Line.Visible = msoTrue
‘Elhagyható (9)Selection.ShapeRange.Line.Style = msoLine
ThinThin ‘Kettős vékony vonal (10)Selection.ShapeRange.Line.Weight = 3#
‘Vonalvastagság (11)Selection.ShapeRange.Fill.ForeColor.RGB = RGB(255, 204, 153)
‘Elhagyható (12)Selection.ShapeRange.Fill.PresetTextured
msoTextureOak ‘Kitöltés tölgyfa textúra (13)End Sub
‘(14)Az 1 és 14 sorszámú sorok a szubrutin kezdetét ill. végét jelzik. A VBA programok mindig szubrutinok formájában jelennek meg, egy feladathoz több szubrutin is tartozhat. A 2 ... 7 sorok comment-ek, ezek magyarázatul, illetve a program áttekinthető tagolására szolgálnak, a program müködésében nem vesznek részt. A comment-eket a
‘ (felső vessző) jelőli, a sor ez után álló része a comment, amit a VBA szerkesztő rendszere az érdemi programrészektől való megkülönböztetésül automatikusan zőld színnel ír. (Az Excel makrókészítő által írt comment-eket a sorok számozásával és néhány további magyarázattal egészítettük ki, ezeket piros színűre állítottuk. A saját gépben a feljegyzett makrót megnézve csak a zöld comment-ek láthatók, a pirosak nem; a kék színnel jelölt, egyéni válsztástól függő programrészek pedig feketében jelennek meg, persze esetleg más számértékkel ill. szöveggel.)Programunk első működő utasítása a 8 jelű sor, ez rajzolja meg az ellipszist. Érdemes részletesen szemügyre venni, mivel
szerkezete jellemző az alkalmazási rendszer vezérlését végző VBA utasításokra. Az első két tag ActiveSheet.Shapes azt mondja meg, hogy mi az, amit módosítani kívánunk. Az ActiveSheet az Excel rendszer megnyitott munkafüzetének éppen munkában lévő (aktív) munkalapjához tartozó adatok összességét (collection) jelenti. Ezen belül az adatok fajtánként alcsoportokat alkotnak. Mi most a rajzi alakzatok alcsoportjával foglalkozunk, ezt határozza meg a Shapes kifejezés. A két kifejezést . (pont) választja el, ez úgy értelmezendő, hogy a ponttól balra álló (esetleg szintén összetett) kifejezés a nagyobb adatösszesség, a jobbra álló pedig ennek egy részét jelöli ki. Az ActiveSheet.Shapes még maga is összesség, collection, hiszen az Excel-ben egy-egy munkalapon nagyszámú rajzi alakzatot jeleníthetünk meg. AddShape(msoShapeOval, 157.8, 259.8, 133.2, 73.2) kifejezés a tulajdonképpeni módszer (method), amellyel létrehozzuk az ellipszist, és új alakzatként hozzáadjuk az előtte álló ponttól balra megnevezett collection-hoz, esetünkben az adott munkalap rajzi alakzatainak összességéhez. A zárójelen belül elsőnek a rajzi alakzat fajtáját kell egy szabványos "szóval" megadni, az ezt követő négy valós szám pedig rendre az ellipszist befoglaló téglalap bal felső sarkának x és y koordinátája, majd pedig a befoglaló téglalap x irányú ill. y irányú mérete. (Mivel az ellipszist "szemre" rajzoltuk be, a számértékek a hely és a nagyság ilyen megválasztásának az "esetlegességét" tükrözik.)Az
ActiveSheet.Shapes.AddShape (msoShape Oval,157.8, 259.8, 133.2, 73.2) háromtagú kifejezés most már egyetlen rajzi alakzatot, shape-t jelent, nevezetesen az éppen nyitott munkalapon megjelenítendő alakzatok összességéhez újonnan hozzáadott ellipszist. Mint minden objektumnak, ennek is vannak tulajdonságai (properties). Tudjuk, hogy a vektorgrafikus rendszereknél kiválaszthatunk egy vagy több alkzatot, módosítás céljából. Azt, hogy valamely alakzat éppen ki van-e választva, vagy sem, a VBA az alakzat (átmeneti) tulajdonságának tekinti. Programunk 8 jelű sorának utolsó tagja a .Select éppen azt a tulajdonságot fejezi ki, hogy az Excel a frissen létrehozott alakzatot egyben "kiválasztottnak" tekinti, lehet vele tovább dolgozni. Az, hogy a tulajdonságokat ugyanúgy ponttal elválasztva tüntetjük fel, mint amikor egy nagyobb adatösszesség egy kisebb alcsoportjára utalunk, igen logikus a gépi adatszerkezet szempontjából. Ami számunkra egy objektum, pl. látványként egyetlen ellipszis, az a gépben tárolt adatstruktúra szempontjából még mindíg egy (számos minőségi és számszerű adatot tartalmazó) adatcsoport, amiből egy tulajdonság kiválasztása egyszerűen az éppen használni kívánt adatok körének további leszűkítése. Az összetett adatstruktúrák kezelésének ezt a most megismert "elválasztó pontos" leírási rendszerét nem csak a VBA, hanem több más fejlett programnyelv is alkalmazza.A program hátralévő (9...13 jelű) sorai az ellipszis körvonalának és kitöltésének leírására szolgálnak, a piros comment-ek szolgáltatják az egyes sorok magyarázatát. A sorok elején a
Selection.ShapeRange kifejezés adja meg, hogy a 8 jelű sorral létrehozott és egyben ki is választott alakzattal kívánunk foglalkozni. A Range itt csoportot jelent, nevezetesen a kiválasztott alakzatok csoportját, ami esetünkben csak egy kiválasztott elemet tartalmaz, de a VBA a kiválasztással kapcsolatban akár egy, akár több objektum van kiválasztva, mindenképpen ezt a kifejezést használja. A programsorok az alakzat két tulajdonságának, nevezetesen a Line –nak és a Fill –nek a beállítását végzik, ami – legalább is a körítővonal, a Line esetében – ujabb (ismét ponttal elválasztott) "részletes tulajdonságok" (Visible, Style, Weight) értékének a megadásával történik. Az értékadás jele a VBA-ban az = egyenlőségjel, ennek a baloldalán megjelölt változó (tulajdonképpen tárolóhely) felveszi a jobboldalon megadott "értéket", ami lehet számszerű vagy szöveges. A Style tulajdonságnál ez az érték esetünkben az msoLineThinThin (kettős vékony körvonal). A vonalvastagság számértékben adandó meg nyomdai pontokban (mint pl. a betűméret is). A szám után álló # jel azt jelenti, hogy a VBA rendszer itt egy dupla pontosságú helyiértékes törtet vár, ezért arra utasítjuk, hogy beírt, formájában egész szám alakú adatot tekintse ilyennek.Kissé eltérő a programszerkezet a kitöltési minta, a
Fill esetében, amelynél a rendszer a minél szabadabb szín ill. textura definiálás érdekében más formát alkalmaz. Ennek elemzésétől eltekintünk, inkább azt ajánljuk, hogy ha valamely Excel megoldás VBA programban való felhasználásánál probléma merül fel, "játsszuk le" a kívánt megoldást az Excel hagyományos, kézi vezérlésével, és készítessük el a makróját. Így mindig kaphatunk egy szabályos VBA alakot, amit aztán – szükség szerint módosított formában – beépíthetünk a készülő programunkba.Azt is észrevehetjük, hogy az automatikusan írt makrók nem mindig adják a legcélszerűbb programozási megoldást. A mintaprogramban két sort (nevezetesen a 9 és 12 jelűeket) is elhagyhatónak jeleztünk. Nem a legcélszerűbb az a megoldás sem, hogy a makróként automatikusan elkészülő VBA program az új alakzatot mindjárt kiválasztottnak tekinti (ahogyan ez kézi munkánál automatikusan történik), és a kiválsztott alakzatot mint ilyent módosítja. A VBA programírás során a kiválasztást a
With ... End With kulcsszavak alkalmazásával kiválthatjuk. Ha az editált makró 8 ... 13 jelü sorait az alábbi programsorokra módosítjuk, az eredetivel azonos eredményt adó szubrutint kapunk az asztal megrajzolására.With
ActiveSheet.Shapes.AddShape(msoShapeOval, 157.8, 259.8, 133.2, 73.2).Line.Visible = msoTrue
.Line.Style = msoLineThinThin
.Line.Weight = 3#
.Fill.PresetTextured msoTextureOak
End With
Figyeljük meg, hogy a VBA a kulcsszavait (ha azokat helyesen alkalmaztuk, s a szerkesztőrendszer elfogadhatónak találta) automatikusan (sötét)kék színnel írja. Az új programváltozat úgy működik, hogy a
With kulcsszó sorában a kulcsszó után megadott objektumot veszi alapul, s az End With –ig következő sorokat erre az objektumra vonatkoztatva hajtja végre, azaz a With után álló objektumot mindig "odaértelmezi" az End With-ig található sorok elején álló pontok elé.
1.2 A
fotel makró. Változók. Szubrutin paranéterekkel.
A tárgyalóasztal körül elhelyezendő körfotelok VBA leírását ugyanúgy egy makró elkészíttetésével kezdjük, mint az asztal esetén.
1. Rajzoljunk körlapot, az ellipszis ikonra klikkelve, de a
2. A rajzi menüsor
AutoShapes/Basic Shapes almenüjéből válasszuk ki a körgyűrűcikk alakot, és tetszőleges helyen és méretben rajzojunk egyet. Válasszunk ennek is kitöltést és mindjárt forgassuk is el a Draw/Rotate or Flip/Free Rotate eszközzel (erre szükség lesz az asztal körüli elhelyezésnél). Végül zárjuk a makrót.A két esetleges helyzetű és méretű elem természetesen még nem adja ki a fotel alaprajzi jelét. Editáljuk a makrót és a két önálló alakzat VBA programjába belejavítva alakítsuk ki a fotelt. Vegyük figyelembe, hogy a székek elhelyezésénél majd a középpontjukkal lesz célszerű dolgozni, míg a VBA leírás a befoglaló téglalapok bal felső sarkának (az ábrán barna ill. okkersárga pontokkal jelölve) koordinátáit várja adatként. Így az alább látható program a fotel középpontjának x és y koordinátáit, az elforgatás fi szögét, valamint a befoglaló négyzet c oldalhosszát várja adatként. A geometriai viszonyokat az ábra szemlélteti.
Sub
fotel(c As Double, fi As Double, x As Double, y As Double)'
' fotel Macro
' Macro recorded 1/14/02 by Peredy Jozsef
'
' Keyboard Shortcut: Ctrl+f
'
ActiveSheet.Shapes.AddShape(msoShapeOval, x - 0.9 * c / 2, _
y - 0.9 * c / 2, c * 0.9, c * 0.9).Select
Selection.ShapeRange.Fill.ForeColor.RGB = RGB(255, 230, 140)
ActiveSheet.Shapes.AddShape(msoShapeBlockArc, x - c / 2, _
y - c / 2, c, c).Select
Selection.ShapeRange.Fill.ForeColor.RGB = RGB(128, 64, 0)
Selection.ShapeRange.Adjustments.Item(1) = 220#
Selection.ShapeRange.Adjustments.Item(2) = 0.36
Selection.ShapeRange.IncrementRotation fi
End Sub
A körgyűrűcikk megrajzolásánál a fenti ábrán zöld színnel jelölt fogópont mozgatásával lehetett a körgyűrű vastagságát és a cikk nyílászögét szabályozni. A programban ez az
Adjustments (igazítások) tulajdonság formájában jelenik meg. Ez egy – esetünkben két Item-et, tagot tartalmazó – collection, amely a fogópont polárkoordinátáit adja meg, az r sugarat (a külső átmérőhöz viszonyított arányszám formájában) a középponttól, a szöget pedig a jobbra mutató vizszintes tengelytől mérve (értelmes értékeik 90ş < Item(1) < 270ş, 0 < Item(2) < 0.5). Az Item() módszer (method) általánosan használható mindakkor, amikor egy összesség valamely tagjára kell hivatkozni. A gömbölyű zárójelben most a hivatkozott tag sorszáma áll, de név is írható, ha ez ismert (pl. a Name tuljdonságnak való értékadással mi magunk neveztünk el egy objektumot).Azt is láthatjuk, hogy a VBA programunkban betűjeleket alkalmaztunk. Egyrészt így lehetett a két alakzat összeillesztését legvilágosabban megoldani, másrész a tárgyalóasztal körül számos fotelt kell majd elhelyezni, mindegyiket más-más helyre, tehát mindenképpen szükség van arra, hogy a középponti koordinátákat és az elfodítás mértékét változóaknak tekintsük. A VBA – mint minden programnyelv – természetesen lehetőséget ad változók alkalmazására. A jelen szubrutinban a változók olyanok, hogy értéküket kívülröl (mint látni fogjuk egy másik szubrutinból) kell majd megadni. Az ilyen változókat a szubrutin paramétereinek nevezzük. A paramétereket a szubrutin megnevezése utáni gömbölyű zárójelpár közé kell beírni. Minden változónak meg kell adni a nevét és típusát. A VBA-ban a nevek betűvel kezdődhetnek, legfeljebb 255 karakterből állhatnak, nem szakíthatja meg azokat szóköz és nem tartalmazhatják a következő hat karakter egyikét sem: .(pont), !, @, &, $, #. A változó típusát az
As (mint) kulcsszó után kell megadni egy szabvány megnevezéssel (ami szintén kulcsszó). A lehetséges szabvány típusneveket a programírás során a VBA szerkesztőrendszer automatikusan megmutatja, nekünk csak választani kell. A leggyakrabban a Double (dupla pontosságú tizedestört szám), az Integer (egész szám) és a String (szöveg) típusok használatosak. Vegyük észre, hogy miután a makró neve utáni zárójelpár nem üres, a makró már önállóan nem futtatható le (hiszen szükség van a paraméterek valamilyen konkrét értékére). Ezért a közölt szubrutin kipróbálása (és szerkesztése) csak a teljes tárgyaló tervezését végző szubrutinból lehetséges.
1.3 A
targyalo szubrutin. A Dim utasítás. Kapcsolat az Excel celláival. Szubrutinhívás. Ciklusszervezés.A
targyalo szubrutin feladata, hogy a munkalap egy megfelelő helyére elhelyezzen egy kívánt méretű asztalt (az asztal szubrutinnal), és ezt körülrakja előírt számú ülőhellyel (a fotel szubrutin felhasználásával). Az 1.1 alatt elkészített asztal szubrutin azonban eredeti formájában csak egy bizonyos helyre egy bizonyos fix méretű asztalt tud rajzolni, ezért ezt is a fotel szubrutinhoz hasonló paraméteres alakra célszerű hozni. A módosuló két sor a következő:Sub
asztal(a As Double, b As Double, x0 As Double, y0 As Double)ActiveSheet.Shapes.AddShape(msoShapeOval, x0 - a / 2, y0 - b / 2,_
a, b).Select
Itt a és b az ellipszis asztal vizszintes ill. függőleges kiterjedése, x0 és y0 pedig középpontjának koordinátái.
A
targyalo szubrutin létrehozásához nyissuk meg a Tools/Macro/ Macros... utasítással a makrók kezelését végző ablakot, irjuk be a megírni kívánt szubrutin nevét (targyalo) és klokkeljünk a Create -re. Ekkor létrejön az új szubrutin váza, amit Edit-álva kitölthetünk a szükséges utasításokkal, comment-ekkel.Sub
targyalo()'
' targyalo Macro
' Macro recorded 2/14/01 by Peredy Jozsef
'
' Keyboard Shortcut: Ctrl+t
' I.) A használt változók dimenzionálása
Dim
a As Double, b As Double, c As Double, m As Double, fir As DoubleDim
x As Double, y As Double, x0 As Double, y0 As Double, fi As DoubleDim
n As Integer, i As Integer' II.) A változók kezdőértékeinek beállítása az Excel megfelelő cellái alapján.
m = Range("G2")
a = m * Range("D3")
b = m * Range("D4")
c = m * Range("D5")
n = Range("D6")
x0 = Range("G4")
y0 = Range("G5")
' III.) Az asztal megrajzolása.
asztal a, b, x0, y0
' IV.) Az n
darab ülőhely elhelyezése az asztal körül.For
i = 0 To n – 1fi = i * 360 / n
fir = -fi * 3.1415962 / 180
x = x0 + (a / 2 + 0.55 * c) * Sin(fir)
y = y0 + (b / 2 + 0.55 * c) * Cos(fir)
fotel c, (fi - 180), x, y
Next
iEnd Sub
A szubrutin – mint látjuk – négy fő részből áll. Ezeket római számozással ellátott commentek jelölik a fenti programban. Az I.) alatti programrész a programban használni kívánt változók deklarálása, ami a VBA-ban a
Dim (dimension) utasítással történik. A Dim utasítás után a változók nevét és típusát kell vesszőkkel elválasztva felsorolni a paraméterek használatánál már megismert rend szerint. Ha a programban olyan név fordul elő, amely sem paraméterként, sem Dim utasítással nem lett elöre megnevezve, a VBA hibajelzést ad. Ez a deklarálási kötelezettség persze teher a programírás során, és könnyen megoldható lenne, hogy minden új nevet a rendszer automatikusan deklaráljon magának. A deklarálási kötelezettség azonban megkönnyíti a szándékaink szerint működő, helyes programok létrehozását, segít kiküszöbölni a névelírásból származó hibákat.A bemutatott
targyalo szubrutin nem tartalmaz paramétereket, önállóan hívható. Adatokat azonban kell valamilyen módon kapnia, hiszen egyébként csak egy adott méretű asztalt tudna rajzolni, körülötte egy bizonyos darabszámú ülőhellyel. A "bemenő adatok" megadását most az Excel segítségével oldottuk meg, az Excel aktív munkalapjának egyes kijelölt celláiba kell a tárgyaló kívánt adatait beírni. Az 1. feladat tárgyalásának elején álló ábra szemlélteti azt az Excel munkalapot, amire a bemutatott program vonatkozik. A targyalo szubrutin II.) alatti programrésze adja át az Excel cellákba beírt értékeket a megfelelő változóknak. Például azm = Range("G2")
sor azt jelenti, hogy az m nevű változó felveszi az éppen aktiv munkalap G2 cellájában található értéket. (Mindezt részletesen is kifejthettük volna:
ActiveSheet.Range("G2").Value, a rendszer azonban többnyire megengedi, hogy a "kézenfekvő" információk kiírásától eltekintsünk.) Az azonban szigorú megkötés, hogy a Range utáni zárójelben szövegnek (string) kell állni, ezt jelzi a G2 cellacím előtt és után az idézőjel. Az m változó egyébként eddig nem szerepelt (és nem is tartozik a dolog lényegéhez), de segítségével beállíthatjuk az ábra méretét, hogy pl. igen nagy tárgyalóasztal esetén is jól áttekinthető maradjon. A többi változó beállítása ezek után magától értetődő.A szubrutinunk III.) része egyetlen sor, nevezetesen az
asztal szubrutin meghívása. Egy szubrutin meghívása azt jelenti, hogy a hívó programban (ami esetünkben a targyalo) az adott helyen elvégeztetjük mindazt, ami a meghívott szubrutinban le van programozva (esetünkben megrajzoltatjuk az asztalt). Ha a hívott szubrutinnak vannak paraméterei, akkor a meghíváskor a név megadása után pontosan annyi és olyan típusú értéknek kell állnia, mint amit a paraméterek megkívánnak. Az érték lehet konkrét szám, vagy szöveg, illetve olyan változó, amely a psrogram futása során már korábban megfelelő értéket kapott. Esetünkben mind a négy paraméter változók révén kap értéket, e változók azonban a programban néhány sorral fentebb már szerepeltek értékadó utasítások bal oldalán, azaz maguk is értéket kaptak az Excel megfelelő celláiból. Figyeljük meg azt is, hogy a szubrutin megírásakor a paramétereknek zárójelben kell a név után állniok, de amikor a szubrutint a nevével meghívjuk, akkor a paraméterek felveendő értékeit a VBA-ban zárójel nélkül kell felsorolni.A program utolsó, IV.) alatti része a programozás egyik alpvető módszerét, a ciklusszervezést mutatja be. Esetünkben arról van szó, hogy számos széket kell más-más helyen és elfordítással az asztal köré elhelyezni, azaz ugyanazt a jellegű feladatot kell némileg változott formában ismételten végrehajtani. A ciklust a
For i = 0 To n – 1 ciklusindító és a Next i cikluszáró utasítások szervezik meg. Ezek hatására az i változó (ezt nevezik ciklusváltozónak) felveszi először is a 0 értéket, majd az 1-et, a 2-t, és így tovább egyesével növekedve utoljára az (n-1)-et, és végrehajtja i minden egyes értékére nézve a For és a Next közötti utasításcsoportot (ez a ciklus magja). Az ülőhelyekkel az asztal teljes kerületét körbe kívánjuk rakni, ezért a 360 fokot az ülőhelyek kívánt darabszámának megfelelöen n részre osztjuk. (A késöbbiekben más elhelyezési módszereket is vozsgálni fogunk.) Ennek megfelelően a ciklusmag kiszámolja az i-edik ülőhely helyzetét megszabó fi szöget (először fokokban majd radiánban), majd meghatározza az éppen elhelyezés alatt álló körfotel alaprajzi középpontjának koordinátáit az ellipszis ismert paraméteres képletével, végül meghívja a fotel szubrutint. Az ellipszis egyenletének paraméteres alakja a megszokottabb matematikai írásmóddal: x = x0+a' sin j , y = y0+b' cos j . Mivel a körfotelok középpontjai nem illeszkednek az asztal kerületére (alaprajzi vetületben sem), hanem egy annál nagyobb ellipszisen fekszenek a' > a/2 és b' > b/2. Vegyük észre, hogy a VBA-ban a trigonometrikus függvények radiánokkal dolgoznak, a fotel elfordításánál viszont fokot használunk.Ha a kész
targyalo()szubrutint lefuttatjuk, akkor az 1. Feladat elején álló tárgyalóasztal elrendezést nyerjük. Ez természetesen azokhoz a kiindulási adatokhoz tartozik, amelyek az ábrán szerepelnek. Az Excel munkalap árnyalással jelölt celláiban lévő számértékek változtatásával (és persze a korábbi ábra törlésével, valamint a szubrutin újrafuttatásával) több esetre kipróbálhatjuk a program működését. Ennek során azt is megfigyelhetjük, hogy minél nyújtottabb az ellipszis, annál "csúnyábban" osztja ki az ülőhelyeket a program. Egyrészt az asztal "hegyes" végén túl közel kerülnek az ülőhelyek egymáshoz, másrészt a fotelok mind az asztal közepe felé néznek, jóllehet kellemesebb lenne az elrendezés, ha párhuzamosan állnának az asztal peremével.
1.4 A
rendez szubrutin. Az If utasítás. Ívhossz és érintő számítása véges elem módszerrel.Számunkra kézenfekvő, hogy az ülőhelyeket az asztal kerülete mentén egyenletesen osszuk ki, a klasszikus matematika számára azonban ez egyáltalán nem elemi feladat. Az ellipszis ívhosszát leíró integrálokat ugyanis nem lehet az elemi függvényekkel zárt alakban kifejezni, s kialakult az ellptikus integrálok ill. az elliptikus függvények külön elmélete, ami az építészek jórészének az érdeklődésétől eléggé távol áll. A számítógépes megkőzelítésben azonban az egyenletes kiosztás megvalósításának módja ugyanolyan magától értetődő, mint amilyen magátólértetődő magának az egyenletes kiosztásnak az igénye.

Bonyolult matematikai eszközökkel (pl. differenciál- és/vagy integrálegyenletekkel) leírható feladataink számítógépes megoldásánál gyakran alkalmazzuk a "véges elem módszert" mind a geometriai elrendezés, mind a tartószerkezettervezés, vagy valamely épületfizikai elemzés stb. során. Ennek alagondolata a következő. Van egy, a maga egészében nehezen kezelhető feladatunk. Ennek a feladatnak az alkalmazási cél szempontjából kifogástalan (közelítő) megoldását kaphatjuk, ha azt sikerül nagyszámú (de nem végtelen sok), kis (de nem végtelenül kis) elemből összetenni úgy, hogy az egyes véges elemek esetében a feladat megoldása jól ismert, egyszerű, de sokan együtt mégis jellemzik az eredeti bonyolult feladatot. Az ellipszis ívhosszának számításánál az ívet rövid húrokból álló sokszögvonallal helyettesítjük. Az egyes húrok egyenesek, hosszuk a Pitagorasz-tétellel jólismert módon számítható, s ha ezeket az elemi hosszakat összeadjuk, kiadódik az eredeti görbe ívhossza a megkívánt pontossággal:
![]()
A képlet mindjárt az érintő hajlásszögének a közelítő értékét is megadja. A "megkívánt pontosság" kifejezés úgy értendő, hogy az általunk használt számítógépekkel és szoftverekkel a közelítő poligon megfelelő megválasztása (lásd később) mellett az ilyenfajta feladatoknál a műszaki cél által megkívánt pontosság általában elérhető. Az asztal kerülete mentén egyenlő távolságra, az asztalperem érintőjének megfelelő elforgatással történő ülőhelyelrendezést az alábbi szubrutinnal valósíthatjuk meg:
Sub
rendez()' rendez Macro
' Macro recorded 2/14/01 by Peredy Jozsef
' Keyboard Shortcut: Ctrl+r
' I.)
Dim
a As Double, b As Double, c As Double, m As DoubleDim
xi As Double, yi As Double, x0 As Double, y0 As DoubleDim
xn As Double, yn As Double, arct As Double, arca As DoubleDim
arcd As Double, arcl As Double, pi As DoubleDim
fin As Double, fi As Double, fip As DoubleDim
n As Integer, nfin As Integer, i As Integer' II.)
m = Range("G2")
a = m * Range("D3")
b = m * Range("D4")
c = m * Range("D5")
n = Range("D6")
nfin = Range("B7")
x0 = Range("G4")
y0 = Range("G5")
pi = Atn(1) * 4
asztal a, b, x0, y0
' III.)
arct = 0
For
i = 0 To nfin * 360 - 1fi = -i * pi / (nfin * 180)
fin = -(i + 1) * pi / (nfin * 180)
xi = x0 + (a / 2 + 0.55 * c) * Sin(fi)
yi = y0 + (b / 2 + 0.55 * c) * Cos(fi)
xn = x0 + (a / 2 + 0.55 * c) * Sin(fin)
yn = y0 + (b / 2 + 0.55 * c) * Cos(fin)
arct = arct + Sqr((xn - xi) ^ 2 + (yn - yi) ^ 2)
Next
i' IV.)
Range("D7") = arct
' V.)
arcd = arct / n
arcl = arcd
arct = 0
For
i = 0 To nfin * 360fi = i * pi / (nfin * 180)
fin = (i + 1) * pi / (nfin * 180)
xi = x0 - (a / 2 + 0.55 * c) * Sin(fi)
yi = y0 + (b / 2 + 0.55 * c) * Cos(fi)
xn = x0 - (a / 2 + 0.55 * c) * Sin(fin)
yn = y0 + (b / 2 + 0.55 * c) * Cos(fin)
arct = arct + Sqr((xn - xi) ^ 2 + (yn - yi) ^ 2)
' VI.)
If
arct > arcl Thenfip = Atn((yn - yi) / (xn - xi)) * 180 / pi
If
xn - xi < 0 Then fip = fip + 180fotel c, fip, xi, yi
arcl = arcl + arcd
End If
Next
iEnd Sub
A szubrutin a
' I.) …' VI.) római számozással az áttekinthetőség érdekében részekre van osztva, és ezekhez kölön-külön fűzünk magyarázatot.Ad I.) E részben találjuk a használt változók deklarálását. A deklaráló rész – jóllehet rendszerint a program elején áll – többnyire utólag, az érdemi részek megírása után készül, amikor már egyértelmű, hogy a feladat megoldásához milyen változókat kell használnunk.
Ad II.) Ez a rész a változók kezdő értékeit állítja be, túlnyomórészt ugyanúgy az Excel cellákból véve át azokat, mint ahogyan a
targyalo szubrutin edetében már láttuk. Új változó az nfin, ami a kerület- és érintőszámításhoz használni kivánt felosztási finomságot szabja meg. Jelentése az, hogy egy fokot hány részre kívánunk felosztani a kellő pontosságú kerület és érintőszámításhoz. Ha értéke 1, akkor fokonként iktatunk be poligon-csúcspontot az ellipszis kerületére, azaz a teljes ellipszist egy 360 oldalú poligonnal közelítjük, ha pedig nfin =10, akkor tizedfokokkal, azaz 3600 oldalú poligonnal dolgozunk. A változók kezdeti beállításánál az utolsó tétel a pi, azaz p. Mivel tg(45˚) = tg(p/4) = 1, úgy számolhatjuk, hogy vesszük az 1-nek megfelelő arcus tangens négyszeresét. A VBA-ban az Atn függvény képezi az adott tangensértékhez tartozó radiánban értett szögértékeket, mindig -p/2 és +p/2 közötti eredményt adva.Ad III.) Az asztal megrajzolása utáni programrész képezi az ellipszis kerületét. A kerületet az
arct változóban állítja elő elő olymódon, hogy egy annyiszor lefutó ciklust indít, ahány oldala van a közelítő poligonnak, kiszámítja az i ciklusváltozó szerint éppen soron lévő poligon-oldal (ellipszishúr) hosszát, és ezt hozzáadja az arct változó már meglévő értékéhez. Az összegezésnek ez a módja a programokban általánosan használatos, de csak akkor lehetünk biztosak a helyes végeredményben, ha azt a változót, amibe elő kivánjuk állítani az összeget a ciklus indítása előtt azon kívül nullára állítjuk, kinullázzuk. A kinullázás a III) comment-et kovető sorban a beleösszegezés pedig a ciklusmag utolsó sorában történik.Ad IV.) Az itt álló egyetlen sor kiírja a kiszámított kerületet az Excel munkalap egy cellájába, ahol az számunkra is látható formában meg tud jelenni.
Ad V.) Az itt kezdődő hátralévő programrész valósítja meg a székek egyenletes kiosztását az ívhossz mentén. Ennek stratégiája a következő. A teljes ellipszis ívhossza az
arct változóban már megvan, miután a III.) alatti ciklus meghatározta. Ha n darab ülőhelyet kívánunk a tárgyalóasztal körül elhelyezni, a teljes ívhossz n-ed része lesz a két ülőhely közötti ivhossz arcd=arct/n. Kiindulunk a j=0 szögnek megfeleló ellipszispontból, s a fotelok középpontjait rendre az ettől az ívhossz mentén mért arcd, 2*arcd, 3*arcd,… n*arcd távolságra lévő ellipszispontokba helyezzük. Az arcl változót használjuk annak az alapponttól az ívhossz mentén mért mindenkori elhelyezési távolságnak a tárolására, ahova a következő fotelnak kerülnie kell. Az ívhosszat számító ciklus indítása előtt az arcl értékét be kell állítani arcd-re, mivel ide kerül az első fotel, és valahányszor elhelyeztünk egy ülőhelyet, értékét meg kell növelni arcd-vel, mert ennyivel van tovább a következő fotel helye az ellipszisív mentén. Az ívhossz folyamatos számítására ugyanazt az arct változót használjuk mint a III.) alatti részben, de természetesen újra ki kell nullázni. A ciklusmag első sorai végzik az ívhosszámítást, a III.) alatti ciklusban már használt módszerrel.Ad VI.) Itt történik az ülőhelyek elhelyezése. Ülőhelyet ott helyezünk el, ahol az ellipszisív mentén folyamatosan (valójában igen kis, de végesen kis lépésekben) haladva a kiszámított
arct ívhossz éppen túllépi a következő fotel helyét megszabó arcl értéket. (Az arct=arcl egyenlőség fennállása általában nem következhet be, többek között azért sem, mert a haladásunk nem teljesen folyamatos.) A fotel elhelyezése tehát az arct>arcl feltételhez van kötve. A VBA rendszerben az If … Then (Ha … Akkor) kulcsszavak feltételesen végrehajtandó utasítások kifejezésére szolgálnak. Az If és a Then között kell a feltételt kifejező egyenlőtlenségnek állnia (egyenlőségi feltételről csak egész értékű változók körében van értelme beszélni), és a Then után álló utasítások csak akkor hajtódnak végre, ha ez a feltétel igaz ( True logikai értékű). Két alakja van e feltételes szerkezetnek, attól függően, hogy a feltétel fennállása (igaz volta) esetén egy (esetleg egymástól : kettősponttal elválasztva egy sorban elférő néhány) utasítást kell-e végrehajtani, vagy pedig tőbbet. Az egy utasításos esetre a ' VI.) comment utáni harmadik sor mutat példát, itt a fip = fip + 180 értékadó utasítás csak az xn - xi < 0 feltétel igaz volta esetén hajtódik végre, de a következő sorban lévő szubrutinhívás végrehajtása már nem függ ettől a feltételtől. (E sor funkciójára mindjárt visszatérünk.) A "sokutasításos If" alakjára a ' VI.) comment utáni hat sor együtt a példa: ilyenkor a Then után nem állhat semmi a sor hátrelévő részében, viszont kell lennie a program további folyamán valahol egy End If sornak, s a feltétel érvénye a Then és az End If közötti valamennyi utasításra (ez a feltételes utasítás magja) vonatkozik. Esetünkben a feltételes utasítás magja az éppen soronlévő kis húrocska hajlásszógének kiszámításával kezdődik, mindjárt fokokba átszámolva (erre a fotel megfelelő elfordításához van szükség). Emlékezzünk azonban, hogy az arcus tangens függvény igen sokértékű, s a programnyelvekbe beépített megfelelő függvények ennek csak a "főágával" (azaz szögértékben kifejezve rendszerint csak -90˚ és +90˚ között) dolgoznak. Esetünkben viszont a tárgyalóasztalt körbe kell rakni fotelekkel, így a teljes 360˚ -os szögtartományra szükség van. Ezt oldja meg az utasításmag második sora. Programunk egyben arra is példa, hogy feltételes utasítások (és a velük sok szempontból rokon ciklusszerkezetek) tetszés szerint egymásba építhetők, de a belső szerkezet a külső határait persze nem lépheti át. A helyes elfordítási szög kiszámítása után elhelyezhetjük a soronlévő fotelt, és a következő fotel elhelyezéséhez átállíthatjuk az ezt vezérlő arcl változót.1.5 Kísérletek, tanulságok. A közelítés pontossága, a gondolkodás ökonómiája.

A fenti ábra úgy készült, hogy az ábárán szereplő számértékek mellett lefuttattuk a
rendez makrót, majd a középponti koordinátákat (G4:G5 cellák) megváltoztatva lefuttatttuk a targyalo makrót. A kétféle szempontú elrendezés közötti kűlönbség szemléletesen jelentkezik az ábrán.A
rendez makró esetében olyan számítási módszereket alkalmaztunk, amelyeket többnyire közelítő módszereknek neveznek (az érintő hajlásszögét a megfelelő kis húr hajlásszögével, az ellipszisgörbe ívhosszát a beleírt igen sok oldalú húrpoligon oldalhosszainak összegével helyettesítettűk). A számítógépes munkánál igen gyakran fordul elő olyan helyzet, hogy kiszámíttatunk a géppel valamit, de ez nem egészen az amit "tulajdonképpen szeretnénk". Esetünkben "tulajdonképpen" az ellipszis "valódi" ívhosszaival szerettünk volna dolgozni, s e helyett használtuk a húrpoligont. De hát ez az "naív" szándékunk eleve reménytelen volt, hiszen már a körív "valódi" hosszát sem írhatjuk le pontosan, mivel mindig ott van benne a p, ez a nem periodikus végtelen tört, aminek csak néhány jegyével tudunk számolni! A számítógépes módszerek csak ráirányítják a figyelmet az emberi megismerés olyan sajátosságaira, amelyek korábban is jelen voltak, csak legtöbbűnkben nem tudatosodtak. A jelen bekezdés első mondatában a "közelítő módszer" kifejezést azért használtuk bizonyos fenntartással, mert igazából pontos számításokról csak szűk körben beszélhetünk. Pontos gondolatmenet létezik az absztrakt matematikában, de amint számszerűsíteni kell valamit, akár papirra számjegyekkel leírva, akár a számítógép véges sok bit-ből álló regisztereivel kifejezve, az igazi pontosság az egész számok (vagy, ami lényegében ugyanaz, a véges törtek) körére korlátozódik.