Hajlított, kéttámaszú tartó diszkrét, sztochasztikus statikai modellje

avagy

hogyan gyártsunk nyomatékábrát ha túl gyors a számítógépünk?

Várkonyi Péter, házi feladat Informatika tárgyból.

Az informatika tárgy házi feladataként olyan egyszerű, diszkrét, sztochasztikus modellt készítettem, amely alkalmas tetszőleges, tartóra merőleges teher mellett meghatározni egy konzol nélküli kéttámaszú tartó támaszerőit és nyomatékábráját. A nyomatékábra előállítására adott algoritmus konzolra is egyszerűen alkalmazható, de például konzolos kéttámaszú vagy más összetettebb tartóra nem. Valószínűleg lehetne általánosítani az algoritmust ezekre is.

A leírt modellt meg is valósítottam MATLAB R13 környezetben.

1. TÁMASZERŐ SZÁMÍTÁS

Először a kéttámaszú tartó támaszerői és egy másik jelenség közötti matematikai analógiát írom le:

Tekintsünk egy, a bal támasztól k/N távolságra koncentrált egységteherrel terhelt kéttámaszú tartót (1/A ábra). Az egyensúlyi egyenletekből a tartó bal- és jobboldali támaszerői

Tekintsünk egy n részre felosztott egység szakaszt és annak a balvégétől x=k/N távolságra lévő pontból induló diszkrét, véletlen sétát (minden lépésben 50-50% eséllyel 1/N-nel lépünk balra illetve jobbra, lásd 1/B ábra). Ismert dolog, hogy a bolyongás során annak a valószínűsége, hogy a szakasz bal, illetve jobb végét érjük el előbb, 1-k/N, illetve k/N.

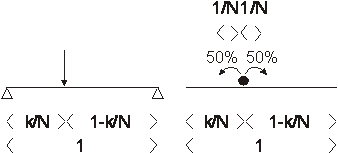
1. ábra. A: kéttámaszú tartó koncentrált erővel. B: diszkrét bolyongás az egységszakaszon

A fenti analógiát és a statikai modell linearitását (két teher összegéhez tartozó támaszerő egyenlő az egyes terhekhez tartozó támaszerők összegével) felhasználva tetszőleges teherrel terhelt kéttámaszú tartó esetén a támaszerőt az alábbi módon közelíthetjük (2. ábra):

- a tehereloszlást diszkretizáljuk, azaz a folytonos terhet egymástól 1/N távolságra lévő koncentrált erőkkel (F₀, F₁,…,F_N) helyettesítjük

- a tehernagyságot is diszkretizáljuk, azaz az összes erőt egy DF elemi erő egész számú többszörösére kerekítjük: F_k»n_k DF.

- Minden lépésben a tartó osztópontjaira elhelyezünk rendre n₀,…,n_N db. „teherkvarkot”, amelyek a továbbiakban egymástól független véletlen sétát végeznek, amíg el nem érik a tartószakasz valamelyik végpontját, akkor pedig eltűnnek.

- Kellően hosszú idő után, a szakasz két végéhez érkező kvarkok aránya a tartó két támaszerejének arányát adja jó közelítéssel.

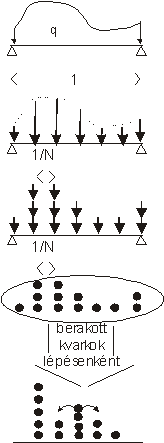
2. ábra. A diszkrét, sztochasztikus modell létrehozásának lépései.

2. NYOMATÉKSZÁMÍTÁS

A nyomatékábra meghatározásához a fenti algoritmust fogjuk követni, de a közelítő eredményt hosszú idő (az egyensúly beállta) után a szakasz egyes pontjaiban található átlagos kvarkszám jelenti majd. Ez az alábbi analógia miatt felel meg a nyomatékábrának, mert:

Legyen egy tartó diszkretizált terhe n₀, n_1,…,n_N nagyságú a diszkrét osztópontokban, a tartó nyomatékai ugyanezen pontokban M₀, M_1,…,M_N. A nyomatéki egyensúly miatt a megoszló teher és a nyomatékábra kapcsolata

aminek diszkrét változata megfelelően átskálázva:

M_k-1+M_k+1-2M_k=n_k

Ha egy szakasz osztópontjaira minden lépésben n₀, n_1,…,n_N kvark érkezik és ezek véletlen bolyongást folytatnak, majd hosszú idő után az egyes pontokban M₀, M_1,…,M_N egyensúlyi kvarkszám lesz, akkor a k. pontba be és kilépő kvarkok egyensúlya miatt:

(M_k-1+M_k+1)/2-M_k+n_k=0

A bal- és jobboldali ablakban lévő egyenlet ekvivalensek. Ezen kívül szükség van még a statikai és a bolyongási feladatot teljessé tevő peremfeltételek ekvivalenciájára:

A kéttámaszú tartó végpontjain a nyomaték 0, azaz

M₀=M_N=0

Mivel a szakasz végpontjait elérő kvarkokat minden lépésben eltüntetjük,

M₀=M_N=0

3. PÉLDÁK

Ebben a részben két konkrét nyomatékszámítási példa szimulációs eredményeit mutatom be (3. és 4. ábra). Látható, hogy a sztochasztikus módszerrel előállított nyomatékábra kellően sok lépés után aránylag jól közelíti a pontos eredményt, de a hiba nagysága nem 0-hoz tart.

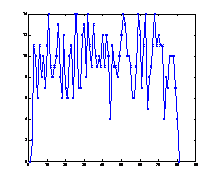
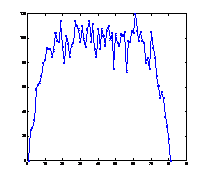
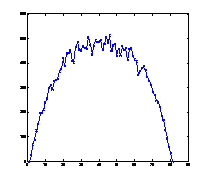
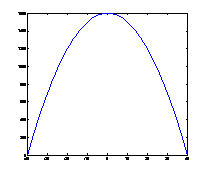
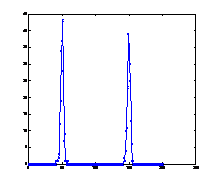
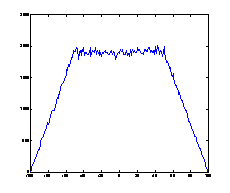
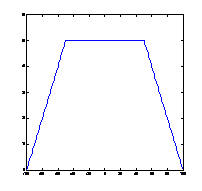
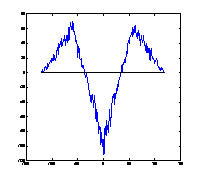
3. ábra: Egyenletes teherrel (1 egység pontonként) terhelt tartó (N=80) nyomatékábrája 10, 100, 500 bolyongási lépés után és a pontos nyomatékábra (analitikusan meghatározva):

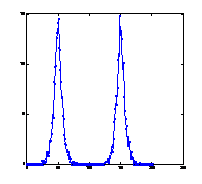
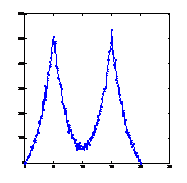
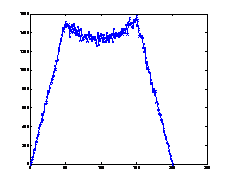
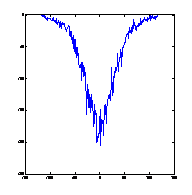
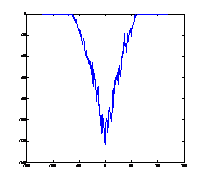
4. ábra: Két koncentrált teherrel (20-20 egység a tartó negyedelőpontjaiban) terhelt tartó (N=200) közelítő nyomatékábrája 10, 100, 1000, 10000, 25000 bolyongási lépés után és a pontos nyomatékábra.

4. AZ ANALÓGIA EGY KORLÁTJA

A fentiekben bemutatott analógia nem teljes, mivel a tartó terhe, illetve nyomatéka pozitív és negatív előjelű is lehet, a kvarkok száma viszont nem lehet negatív. Olyan tartóknál ezért, amelyekre mindkét irányú teher hat, a modell nem értelmes. Ha oly módon általánosítjuk, hogy negatív teher esetén lépésenként nem berakunk, hanem elveszünk kvarkokat, még mindig problémát jelent, ha egy helyen éppen nincs annyi kvark, amennyit el akarunk venni.

Az egyik lehetőség, hogy ha éppen nincs elég kvark, csak annyit veszünk el, amennyi van. Ezzel jó eredményt kapunk, ha a tartón csak egyik irányú nyomaték van (5,6/A ábra), de nem jót ha a keresett nyomatékábra előjelet vált (5,6/B ábra). A másik lehetőség, hogy ilyen esetben bevezetjük a “antikvark” fogalmát, negatív teher esetén lépésenként antikvarkokat helyezünk a szakaszra, és minden lépésben az azonos helyen lévő “rendes” és “antikvarkok” megsemmisítik egymást. Ezzel minden terhelésre a helyes eredmény egy közelítését kapjuk.

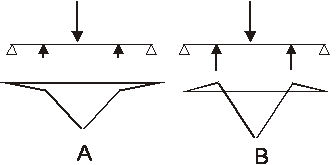
5. ábra: Két példa kétirányú teherrel terhelt tartóra és a nyomatékábrájára

6. ábra: A: Az 5/A ábra tartójának szimulációs eredménye. B: Az 5/B ábra tartójának helytelen szimulációs eredménye. C: Az 5/B ábra tartójának „antikvarkok” alkalmazásával készült helyes szimulációs eredménye.