
A véges elem (finite element) módszer alapgondolata.
A foglalkozás célja, hogy a mérnöki munka számítógépes segítése során napjainkban igen gyakran és széles körben használt véges elem módszer (finite element method) néhány alapkérdésével megismerkedjünk. Mondanivalónk lényegét

a síkbeli feszültségi állapotban lévő tartószerkezetek
(az építészmérnöki munkában ilyenek a faltartók, szélmerevítő falak, stb.) vizsgálata kapcsán mutatjuk be. Például az ábrán látható szélmerevítő fal erőjátékát akkor tekinthetjük ismertnek, ha a fal bármely P(x,y) pontjában tudjuk, mennyi az adott terhek hatására ott keletkező, és pontról pontra folyamatosan változó sx , a sy és a txy feszültség. Ezt a feladatot a klasszikus rugalmasságtan keretében egy negyedrendű parciális differenciálegyenlet segítségével írják le. Ennek zárt alakban, vagy a klasszikus sorfejtéses közelítő módszerekkel való megoldása azonban, még az olyan hétköznapi esetben is, mint az ábrán mutatott merevítőfal, gyakorlatilag kizárt. Így mindenképpen csak arról lehet szó, hogy a szóbanforgó feszültségeket leíró függvények helyett a feszültségek közelítő számértékeit néhány jellemző pontban valamely gépi számításra alkalmas numerikus módszerrel (pl. az említett differenciálegyenlet közelítéseként adódó véges differenciák alkalmazásával) meghatározzuk. Kézenfekvő a gondolat, hogy nem lehetne-e valamiféle számítógépes megoldást lehetőséget találni közvetlenül a fizikai modellre alapozva, a matematikai "kerülőút" mellőzésével. Egy ilyen, széles körben alkalmazott, jól bevált lehetőséga véges elem módszer. Tekintsük az előző ábra jobboldali részét, amely azt mutatja, hogy a vizsgálandó falat kis (háromszögű) részekre osztjuk fel. (A felosztás a teljes falra kiterjed, az ábra csak a bal felső saroktól kiindulva egy darabon tünteti fel a kis területelemeket.) Feltesszük, hogy az egyes elemeken belül a sx , a sy és a txy feszültség (és ezzel együtt az ex , a ey és a gxy fajlagos alakváltozás) állandó, továbbá, hogy az elemek nem folytonosan, hanem csak sarokpontjaikon kapcsolódnak, mégpedig csuklósan. A sarokpontokon az elemek egy-egy függőleges és vizszintes erőt adnak át egymásnak és a kapcsolódó elemek függőleges és vizszintes elmozdulása a sarokpontokban (és csak ott) az alakváltoasok során mindig megegyezik. A feladat megoldása a mozgásmódszer alapján történik: a csomópontok elmozdulásait tekintjük ismeretleneknek és ezen elmozdulásértékeket a csomópontokra vonatkozó egyensúlyi egyenletekből határozzuk meg. E megközelíotésmód nyilván akkor lehet indokolt, ha az elemenként állandónak feltételezett feszültségek elemről-elemre való változása megfelelően nagy (de véges) számú és kis (de nem infinitézimális) méretű elemre való felosztás esetén jól leírja a tényleges szerkezet erőjátékát. Ez mind elméletileg, mind pedig a sokéves széleskörű sikeres gyakorlati alkalmazás alapján igazoltnak tekinthető.

Az említett egyensúlyi egyenletek felállításához ismernünk kell, hogy a csomópontok egységnyi vizszintes vagy függőleges elmozdulása során az egyes véges elemek miként deformálódnak, bennük milyen fajlagos alakváltozások keletkeznek, ezekhez a Hooke törvény alapján milyen feszültségek tartoznak, s a feszültségek eredőjeként végül is milyen csomóponti erők ébrednek. Mindezek a számítások az elemi statikai-szilárdságtani ismereteink alapján elvégezhetők. A végeredmény egy táblázat lesz, amely megmondja, hogy egy véges elem sarokpontjainak elmozdításához milyen csomóponti erők szükségesek. Ez a táblázat
a véges elem merevségi mátrixa.
Esetünkben a véges elemek derékszögű háromszögek, amelyek sarokpontjaikkal csatlakoznak a csomópontokhoz. Mivel minden sarokpontban két-két elmozdulás-összetevőt és két-két erő-összetevőt kell figyelembe vennünk, esetünkben az elemi merevségi mátrix 6x6 -os lesz. Vizsgáljuk először az egyik hegyesszögű sarokpont egységnyi elmozdulásait!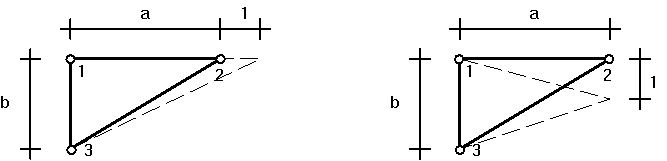
A baloldali ábrán a 2 sarokpont egységnyi vizszintes elmozdítása látható. Az ehhez tartozó fajlagos alakváltozások
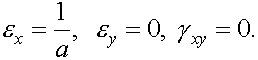
A Hooke törvény szerint ebből kiszámíthatjuk az egységnyi vizszintes elmozduláshoz tartozó feszültségeket:
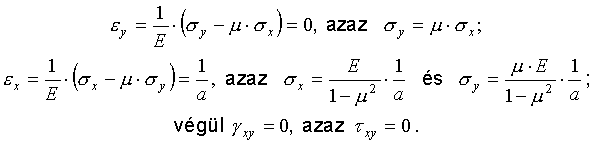
A 2 sarokpont egységnyi függőleges elmozdulásához tartozó fajlagos alakváltozások még egyszerűbben számíthatók:
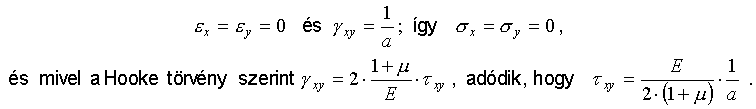
Az alábbi két ábrán feltüntettük a szóbanforgó két alakváltozási esethez (nevezetesen a 2 sarokpont egységnyi vizszintes és függőleges elmozdulásaihoz) tartozó most kiszámított feszültségeket:
 Az ábrák úgy értendők, hogy míg az 1-2 és 1-3 oldalakon ténylegesen az ott feltüntetett feszültségek működnek, addig a 2-3 oldalon az oldal mentén fellépő feszültségek vizszintes és függőleges összetevői láthatók az oldal vizszintes ill. függőleges vetületére rajzolva.
Az ábrák úgy értendők, hogy míg az 1-2 és 1-3 oldalakon ténylegesen az ott feltüntetett feszültségek működnek, addig a 2-3 oldalon az oldal mentén fellépő feszültségek vizszintes és függőleges összetevői láthatók az oldal vizszintes ill. függőleges vetületére rajzolva.
Az elemek azonban nem illeszkednek oldalaik mentén, csak a csomópontokban vannak sarokp[ontjaikkal összekapcsolva, tehát erőket is csak itt adhatnak át egymásnak. A megoszló feszültségeket ezért velük valamilyen értelemben egyenértékű csúcsponti erőkkel kell helyettesítenünk:
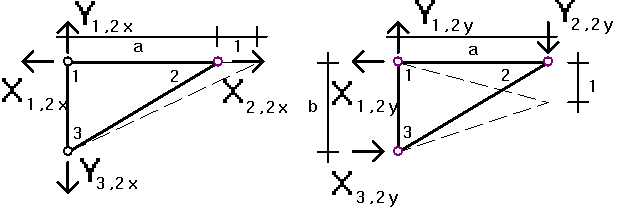
Az erők megnevezésénél a hely-ok jelölésmódot követtük, így pl. Y
1,2x az az 1 sarokpontban ébredő függőleges erő, amely a 2 sarokpont (egységnyi) vizszintes elmozdításához tartozik. A statikai egyenértékűség biztosításának egy "kézenfekvő" módja, ha egy-egy oldalon az ott működő feszültségek eredőjének felét működtetjük az oldal egyik és felét a másik végpontjában, pl.:
Itt feltettük, hogy az elem t vastagsága állandó, és a jobbra ill. lefelé mutató erőket tekintettük pozitívnak. Az ábrán feltüntetett többi erőértéket hasonló módon kiszámolva nyerjük az elem merevségi mátrixának a 2 sarokpont elmozdulásaihoz tartozó két középső oszlopát. A zérus erők úgy adódnak, hogy a ferde oldalon ébredő feszülktségek megfelelő komponense esetenként éppen ellentettje a csatlakozó másik oldalból származó erőnek. (Megjegyzendő, hogy a megoszló feszültségeket helyettesítő csomóponti erők megállapítása általában mélyebb szilárdságtani megfontolásokat igényel, azonban ezek végeredménye a vizsgált egyszerű esetben egybeesik a bemutatott "kézenfekvő" eredőfelezéssel.)
Az elem teljes merevségi mátrixának felállításához további számítás már nem szükséges. A 3 sarokpont az elemnek ugyanolyan jellegű pontja, mint a 2, csak az az eltérés, hogy az 1 -hez képest nem x, hanem y irányban fekszik. Így az x és y, a X és Y, valamint az a és b követekezetes felcserélésével a 2 sarokpont két oszlopából megkaphatjuk a 3 sarokpont két oszlopát.. Az 1 sarokpont oszlopait pedig abból a megfontolásból nyerjük, hogy ha x
1= x2= x3=1 és y1= y2= y3=0 , vagy x1= x2= x3=0 és y1= y2=y3=1, akkor az elem verevtest-szerű elmozdulást végez, nem deformálódik, nem ébrednek benne feszültségek, és így a sarokponti erők is nullára kell, hogy adódjanak. Az elem merecségi mátrixa tehát
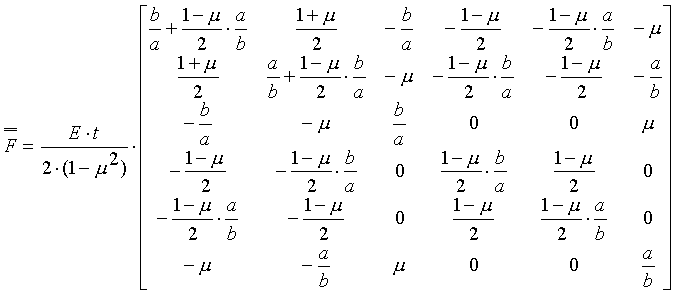 .
.
Ha megfigyeljük a példának vett faltartó végeselem felosztását láthatjuk, hogy a most tárgyalt helyzetű véges elemek mellett még ezeknek az átfogóra vett tükörképei is előfordulnak. Ha azonban ez utóbbiaknál is azt a sorszámozást követjük, hogy az 1 jelű sarokpont a derékszögű, a 2 ehhez képest x irányban, a 3 pedig y irányban helyezkedik el, akkor az ilyen helyzetű elem elemi merevségi mátrixa is ugyanaz lesz, mint a fentebb részletesen vizsgált elemé. Ennek belátására tekintsük az a és b mennyiségeket, mint a 2 és 3 sarokpontoknak az 1 -hez viszonyított előjeles (relatív) koordinátáit. A tükörképi elemnél mind a, mind pedig b előjelet vált, mivel azonban képleteinkben csak a hányadosuk szerepel, világos, hogy a merevségi mátrixban semmi sem változik. Ezek szerint a bemutatott végeselem felosztásban előforduló valamennyi elefajta elemi merevségi mátrixát ismerjük, és így nekiláthatunk a csomópontok egyensúlyát kifejező egyenletrendszer egütthatóinak, azaz
a teljes szerkezet globális merevségi mátrixának
a kiszámításához. Ha egy csomópont egységnyivel elmozdul vizsztes vagy függőleges irányban, akkor mindazok az elemek, amelyek valamelyik sarokpontjukkal e csomóponthoz csatlakoznak, deformálódnak. E deformációkhoz az elemi merevségi mátrix szerinti sarokponti erők tartoznak, a csomópontra ezen erők összege fog működni. A szerkezet globális merevségi mátrixának felállítása tehát mindössze abból áll, hogy az végeselemekre vonatkozó merevségi mátrixok megfelelő elemeit össze kell adni úgy, ahogyan a csomópontokhoz való csatlakozásuknak megfelelően összetartoznak.Természetesen a globális merevségi mátrix felállítását is a számítógéppel kívánjuk végeztetni (a gyakorlat igényeinek megfelelő, sok száz, vagy akár sok ezer véges elemet tartalmazó valós feladatoknál ez nem is lehet másként). E célból a szerkezetnek a végeselem felosztás során adódó csomópontjait sorszámozással kell ellátni, s fel kell sorolni, hogy az egyes elemek sarokpontjai (az elemi merevségi mátrixok felállítása során követett számozás sorrendjében) mely sorszámú csomópontokhoz csatlakoznak. Ezt a felsorolást nevezzük a szerkezet topológiai mátrixának. Maga a felállítás úgy történik, hogy sorravesszük a végeselemeket, minden egyes elemre vonatkozóan a topológiai mátrixban megnézzük, hogy sarokpontjaival mely csomópontokhoz csatlakozik, és a globális mátrix megfelelő helyeire "beleösszegezzük" az elemi mátrix odatartozó értékeit. (A felállítás technikájának bizonyos további részleteire a bemutatandó számpélda is rávilágít.) A globális merevségi mátrixra azért van szükség, hogy felírhassuk a szerkezet
egyensúlyi egyenletrendszerét.
Ez n számú csomópont esetén a következőképpen alakul:|
a11.x1+ |
a12.y1+ |
a13.x2+ |
a14.y2+ |
. . . |
a1 2n-1.xn+ |
a1 2n.yn |
= Fx1 |
|
a21.x1+ |
a22.y1+ |
a23.x2+ |
a24.y2+ |
. . . |
a2 2n-1.xn+ |
a2 2n.yn |
= Fy1 |
|
a31.x1+ |
a32.y1+ |
a33.x2+ |
a34.y2+ |
. . . |
a3 2n-1.xn+ |
a3 2n.yn |
= Fx2 |
|
a41.x1+ |
a42.y1+ |
a43.x2+ |
a44.y2+ |
. . . |
a4 2n-1.xn+ |
a4 2n.yn |
= Fy2 |
|
: |
|||||||
|
a2n-1 1.x1+ |
a2n-1 2.y1+ |
a2n-1 3.x2+ |
a2n-1 4.y2+ |
. . . |
a2n-1 2n-1.xn+ |
a2n-1 2n.yn |
= Fxn |
|
a2n 1.x1+ |
a2n 2.y1+ |
a2n 3.x2+ |
a2n 4.y2+ |
. . . |
a2n 2n-1.xn+ |
a2n 2n.yn |
= Fyn |
Ezt az egyenletrendszert a szakirodalomban inkább mátrixos alakban célszerű felírni:
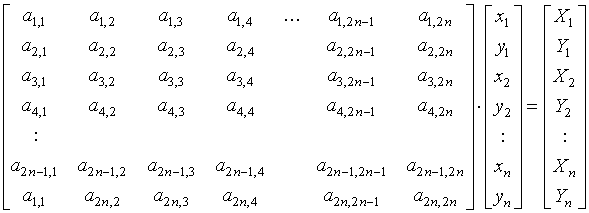 .
.
Az a
i,j ( i=1, 2, ... 2n; j=1, 2, ... 2n ) elemekből álló négyzetes mátrix az egyenülyi egyenletrendszer együttható mátrixa, más szóval a szerkezet globális merevségi mátrixa.. Ax xi és yi ( i=1, 2, ... n ) elemekből álló oszlopvektor tartalmazza az egyenlőre ismeretlen csomóponti elmozdulások vizszintes és függőleges összetevőit, az Xi és Yi ( i=1, 2, ... n ) elemekből álló oszlopvektor pedig a szerkezetre ható terheket, a csomópontokra koncentrált vizszintes és függőleges erők formájában.Az egyensúlyi egyenletrendszer megoldására
kifinomult számítógépes módszerek állnak rendelkezésre. Ezek a merevségi mátrixok speciális szerkezetének kihasználásával biztosítják, hogy a sűrű felosztással járó nagy számú ismeretlen esetén is a tárolókapacitás gazdaságos felhasználása mellett és viszonylag rövid számítási idővel eljuthassunk a csomóp[onti elmozdulások meghatározásáig. A mátrix speciális szerkezete abban áll, hogy egyrészt a főátlóra szimmetrikus, másrészt sok zérus elemet tartalmaz, és ezek bizonyos rendszerben helyezkednek el. Gondoljuk csak meg, hogy ha valamely csomópont elmozdul, akkor csak a hozzá kapcsolódó elemekben ébrednek erők, s ezek az elemek csak néhány további szomszédos csomópontot terhelnek. Az összes többi, az elmozdított csomóponthoz elemmel nem kapcsolódó csomóponthoz tartozó együttható zérus lesz. A nem-zérus elemek a főátló körüli sávban helyezkednek el, a szerkezetek globális merevségi mátrixa mindig szimmetrikus sávmátrix:
Erről a látszólag számítástechnikai jellegű részletkérdésről azért érdemes az (építész-) mérnöknek is tudomással bírni, mert a kis sávszélesség előnyös a gépi megoldás során, ugyanakkor nagyban függ a csomópontok sorszámozásának módjától, amire gyakran nekünk, felhasználóknak is befolyásunk van. Ilyenkor arra kell törekednünk, hogy az egy elem által összekötött csomópontok sorszámai közötti maximális különbség a lehető legkisebb legyen. A bemutatott merevítőfal esetében például nyilván sokkal célszerűbb a csomópontokat soronként és nem oszloponként sorszámozni.
Megoldva az egyensúlyi egyenletrendszert rendelkezésünkre állanak a csomópontok elmozdulásai. Ezek alapján a
feszültségek már számíthatók,
hiszen a 3. oldal felső részén a merevségi mátrix számításánál a háromszögelem 2 sarokpontjának egységnyi elmozdulásaihoz tartozó feszültségeket már felírtuk, a 3 és az 1 jelű sarokpontok feszültségei pedig ezekből ugyanúgy adódnak, mint ahogyan a merevségi mátrix esetében is eljártunk. Így végül is a feszültségszámítás egyenletei (mátrixos alakban) a következők: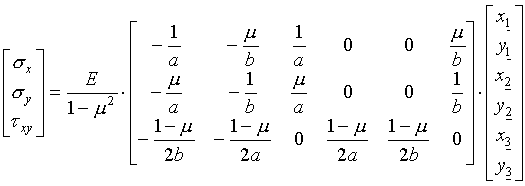 .
.
A fenti képletek akkor adnak előjelben is helyes feszültségi értékeket, ha a -t és b -t a derékszögű háromszög elem 1 jelű sarokpontjához viszonyított előjeles relatív koordinátáknak tekintjük. Az elmozdulás-értékek indexeként 1, 2 és 3 szerepel. A szám aláhúzása arra utal, hogy az elem sarokpontjainak sorszámáról van szó, nem pedig a szerkezet csomópontjainak a sorszámáról, mint az egyensúlyi egyenleteknél. A kettő között - mint már említettük - a topológiai mátrix teremti meg a kapcsolatot.
A feszültségek kiszámításával tulajdonképpen megoldottuk feladatunkat. Végezetül az
általánosítási lehetőségeket
illetően kell néhány megjegyzést tenni. A bemutatott eset, nevezetesen a síkbeli feladat derékszögű háromszöges felosztása, a véges elem módszer egyik legegyszerűbb és letisztább alkalmazása s éppen ezért talán alkalmas arra, hogy a mödszer alapgondolatáról valami fogalmat alkothassunk magunknak. Ugyanakkor tudnunk kell, hogy ilyen egyszerű eset alig van még egy, pl. már a faltartók téglalap elemes megoldása is vet fel olyan elvi problémákat, amelyek esetünkben megkerülhetők voltak. Tovább bonyolódik a helyzet a gyakorlatilag oly fontos lemezek, héjak esetén. A térbeli szilárdságtani feladatok derékszögű tetraéderes felosztása tűnik ki ismét elvi egyszerűségével, tisztaságával. A véges elem módszer összetett feladatokra való hatékony alkalmazása ma már külön tudomány. Az alkalmazási kör is rendkívül széles: a mi szakmánkban említsük csak a tartószerkezetek statikai és dinamikai feladatait, vagy az épületfizikiai vizsgálatokat (pl. hővezetés, hőhidak). De megtaláljuk a véges elem módszereket a természettudományok és a technika szinte minden területén.A véges elem módszer a napjainkban kibontakozó informatikai kultúra jellegzetes eleme. Egyszerű alapelvekre építve a legkülönbözőbb feladatok megoldását foglalja elvileg egységes keretbe, természetesen nagy gépi erőforrások igénybevétele árán. Nagyban előmozdítja korunk egyik fő fejlődési irányát, az emberi gondolkodás hatékonyságának növekedését.
Természetesen a gyakorló szerkezet-tervező általában nem ír végeselemes programokat, hanem a kereskedelmi forgalomban kapható kész programokat használja. Az értelmes és hatékony felhasználáshoz talán segitséget nyújthat ez a kis elvi áttakintés is.
.