BME Építészmérnöki Kar, Építészeti Ábrázolás Tanszék.

CAAD és Építészinformatika, VBA programozás (Excel, AutoCAD)

Előadó: dr. Peredy József prof. em.

2. Feladat. A tárgyalóasztal-elrendezés javítása.

Bármily kézenfekvő, hogy az ülőhelyeket az asztal kerülete mentén egyenletesen osszuk ki, a klasszikus matematikai analízis számára ez egyáltalán nem elemi feladat. Az ellipszis ívhosszát leíró integrálokat nem lehet az elemi függvényekkel zárt alakban kifejezni. Kialakult az ellptikus integrálok ill. az elliptikus függvények elmélete, ami külön tanulmányokat igényel és (elvi szépsége ellenére) számszerű eredmények eléréséhez nem ideális. A számítógépes megkőzelítésben azonban az egyenletes kiosztás megvalósításának módja ugyanolyan egyszerű és természetes, mint amilyen egyszerű és természetes magának az egyenletes kiosztásnak az igénye. Az informatikai kultúra kibontakozásának egyik legfontosabb hozadéka az emberi gondolkodás hatékonyságának növekedése, a „gondolkodás ökonómiája". Ez esetünkben abban jelentkezik, hogy néhány elemi alapelv segítségével a feladatok rendkívül széles körére tudunk megfelelő megoldást találni, így az ellipszis kerületének számítására is.

2.1 A rendez szubrutin. Az If utasítás. Ívhossz és érintő számítása véges elem módszerrel.

Bonyolult matematikai eszközökkel (pl. differenciál- és/vagy integrálegyenletekkel) leírható feladataink számítógépes megoldásánál gyakran alkalmazzuk a "véges elem módszert" mind a geometriai elrendezés, mind a tartószerkezettervezés, vagy éppen valamely épületfizikai elemzés stb. során. Ennek alagondolata a következő. Van egy, a maga egészében nehezen kezelhető feladatunk. Ennek a feladatnak az alkalmazási cél szempontjából kifogástalan (közelítő) megoldását kaphatjuk, ha azt sikerül nagyszámú (de nem végtelen sok), kis (de nem végtelenül kis) elemből összetenni úgy, hogy az egyes véges elemek esetében a feladat megoldása jól ismert, egyszerű, de sok egyszerű véges elem együtt mégis jellemzi az eredeti bonyolult feladatot. Az ellipszis ívhosszának számításánál az ívet rövid húrokból álló sokszögvonallal helyettesítjük. Az egyes húrok egyenesek, hosszuk a Pitagorasz-tétellel jólismert módon számítható, s ha ezeket az elemi hosszakat összeadjuk, kiadódik az eredeti görbe ívhossza a megkívánt pontossággal:

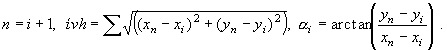
A képlet mindjárt az érintő hajlásszögének a közelítő értékét is megadja. A "megkívánt pontosság" kifejezés úgy értendő, hogy az általunk használt számítógépekkel és szoftverekkel a közelítő poligon megfelelő megválasztása (lásd később) mellett az ilyenfajta feladatoknál a műszaki cél által megkívánt pontosság általában elérhető. Az asztal kerülete mentén egyenlő távolságra, az asztalperem érintőjének megfelelő elforgatással történő ülőhelyelrendezést az alábbi szubrutinnal valósíthatjuk meg:

Sub rendez()

' rendez Macro

' Macro recorded 2/14/01 by Peredy Jozsef

' Keyboard Shortcut: Ctrl+r

' I.)

Dim a As Double, b As Double, c As Double, m As Double

Dim xi As Double, yi As Double, x0 As Double, y0 As Double

Dim xn As Double, yn As Double, arct As Double, arca As Double

Dim arcd As Double, arcl As Double, pi As Double

Dim fin As Double, fi As Double, fip As Double

Dim n As Integer, nfin As Integer, i As Integer

' II.)

m = Range("G2")

a = m * Range("D3")

b = m * Range("D4")

c = m * Range("D5")

n = Range("D6")

nfin = Range("B7")

x0 = Range("G4")

y0 = Range("G5")

pi = Atn(1) * 4

asztal a, b, x0, y0

' III.)

arct = 0

For i = 0 To nfin * 360 - 1

fi = -i * pi / (nfin * 180)

fin = -(i + 1) * pi / (nfin * 180)

xi = x0 + (a / 2 + 0.55 * c) * Sin(fi)

yi = y0 + (b / 2 + 0.55 * c) * Cos(fi)

xn = x0 + (a / 2 + 0.55 * c) * Sin(fin)

yn = y0 + (b / 2 + 0.55 * c) * Cos(fin)

arct = arct + Sqr((xn - xi) ^ 2 + (yn - yi) ^ 2)

Next i

' IV.)

Range("D7") = arct

' V.)

arcd = arct / n

arcl = arcd

arct = 0

For i = 0 To nfin * 360

fi = i * pi / (nfin * 180)

fin = (i + 1) * pi / (nfin * 180)

xi = x0 - (a / 2 + 0.55 * c) * Sin(fi)

yi = y0 + (b / 2 + 0.55 * c) * Cos(fi)

xn = x0 - (a / 2 + 0.55 * c) * Sin(fin)

yn = y0 + (b / 2 + 0.55 * c) * Cos(fin)

arct = arct + Sqr((xn - xi) ^ 2 + (yn - yi) ^ 2)

' VI.)

If arct > arcl Then

fip = Atn((yn - yi) / (xn - xi)) * 180 / pi

If xn - xi < 0 Then fip = fip + 180

fotel c, fip, xi, yi

arcl = arcl + arcd

End If

Next i

End Sub

A szubrutin a ' I.) …' VI.) római számozással az áttekinthetőség érdekében részekre van osztva, és ezekhez kölön-külön fűzünk magyarázatot.

Ad I.) E részben találjuk a használt változók deklarálását. A deklaráló rész – jóllehet rendszerint a program elején áll – többnyire utólag, az érdemi részek megírása után készül, amikor már egyértelmű, hogy a feladat megoldásához milyen változókat kell használnunk.

Ad II.) Ez a rész a változók kezdő értékeit állítja be, túlnyomórészt ugyanúgy az Excel cellákból véve át azokat, mint ahogyan a targyalo szubrutin edetében már láttuk. Új változó az nfin, ami a kerület- és érintőszámításhoz használni kivánt felosztási finomságot szabja meg. Jelentése az, hogy egy fokot hány részre kívánunk felosztani a kellő pontosságú kerület és érintőszámításhoz. Ha értéke 1, akkor fokonként iktatunk be poligon-csúcspontot az ellipszis kerületére, azaz a teljes ellipszist egy 360 oldalú poligonnal közelítjük, ha pedig nfin =10, akkor tizedfokokkal, azaz 3600 oldalú poligonnal dolgozunk. A változók kezdeti beállításánál az utolsó tétel a pi, azaz p. Mivel tg(45˚) = tg(p/4) = 1, úgy számolhatjuk, hogy vesszük az 1-nek megfelelő arcus tangens négyszeresét. A VBA-ban az Atn függvény képezi az adott tangensértékhez tartozó radiánban értett szögértékeket, mindig -p/2 és +p/2 közötti eredményt adva.

Ad III.) Az asztal megrajzolása utáni programrész képezi az ellipszis kerületét. A kerületet az arct változóban állítja elő elő olymódon, hogy egy annyiszor lefutó ciklust indít, ahány oldala van a közelítő poligonnak, kiszámítja az i ciklusváltozó szerint éppen soron lévő poligon-oldal (ellipszishúr) hosszát, és ezt hozzáadja az arct változó már meglévő értékéhez. Az összegezésnek ez a módja a programokban általánosan használatos, de csak akkor lehetünk biztosak a helyes végeredményben, ha azt a változót, amibe elő kivánjuk állítani az összeget a ciklus indítása előtt (azon kívül) nullára állítjuk, kinullázzuk. A kinullázás a III) comment-et kovető sorban a beleösszegezés pedig a ciklusmag utolsó sorában történik.

Ad IV.) Az itt álló egyetlen sor kiírja a kiszámított kerületet az Excel munkalap egy cellájába, ahol az számunkra is látható formában meg tud jelenni.

Ad V.) Az itt kezdődő hátralévő programrész valósítja meg a székek egyenletes kiosztását az ívhossz mentén. Ennek stratégiája a következő. A teljes ellipszis ívhossza az arct változóban már megvan, miután a III.) alatti ciklus meghatározta. Ha n darab ülőhelyet kívánunk a tárgyalóasztal körül elhelyezni, a teljes ívhossz n-ed része lesz a két ülőhely közötti ivhossz arcd=arct/n. Kiindulunk a j=0 szögnek megfeleló ellipszispontból, s a fotelok középpontjait rendre az ettől az ívhossz mentén mért arcd, 2*arcd, 3*arcd,… n*arcd távolságra lévő ellipszispontokba helyezzük. Az arcl változót használjuk annak az alapponttól az ívhossz mentén mért mindenkori elhelyezési távolságnak a tárolására, ahova a következő fotelnak kerülnie kell. Az ívhosszat számító ciklus indítása előtt az arcl értékét be kell állítani arcd-re, mivel ide kerül az első fotel, és valahányszor elhelyeztünk egy ülőhelyet, értékét meg kell növelni arcd-vel, mert ennyivel van tovább a következő fotel helye az ellipszisív mentén. Az ívhossz folyamatos számítására ugyanazt az arct változót használjuk mint a III.) alatti részben, de természetesen újra ki kell nullázni. A ciklusmag első sorai végzik az ívhosszámítást, a III.) alatti ciklusban már használt módszerrel.

Ad VI.) Itt történik az ülőhelyek elhelyezése. Ülőhelyet ott helyezünk el, ahol az ellipszisív mentén folyamatosan (valójában igen kis, de végesen kis lépésekben) haladva a kiszámított arct ívhossz éppen túllépi a következő fotel helyét megszabó arcl értéket. (Az arct=arcl egyenlőség fennállása általában nem következhet be, többek között azért sem, mert a haladásunk nem teljesen folyamatos.) A fotel elhelyezése tehát az arct>arcl feltételhez van kötve. A VBA rendszerben az If … Then (Ha … Akkor) kulcsszavak feltételesen végrehajtandó utasítások kifejezésére szolgálnak. Az If és a Then között kell a feltételt kifejező egyenlőtlenségnek állnia (egyenlőségi feltételről csak egész értékű változók körében van értelme beszélni), és a Then után álló utasítások csak akkor hajtódnak végre, ha ez a feltétel igaz ( True logikai értékű). Két alakja van e feltételes szerkezetnek, attól függően, hogy a feltétel fennállása (igaz volta) esetén egy (esetleg egymástól : kettősponttal elválasztva egy sorban elférő néhány) utasítást kell-e végrehajtani, vagy pedig tőbbet. Az egy utasításos esetre a ' VI.) comment utáni harmadik sor mutat példát, itt a fip = fip + 180 értékadó utasítás csak az xn - xi < 0 feltétel igaz volta esetén hajtódik végre, de a következő sorban lévő szubrutinhívás végrehajtása már nem függ ettől a feltételtől. (E sor funkciójára mindjárt visszatérünk.) A "sokutasításos If" alakjára a ' VI.) comment utáni hat sor együtt a példa: ilyenkor a Then után nem állhat semmi a sor hátrelévő részében, viszont kell lennie a program további folyamán valahol egy End If sornak, s a feltétel érvénye a Then és az End If közötti valamennyi utasításra (ez a feltételes utasítás magja) vonatkozik. Esetünkben a feltételes utasítás magja az éppen soronlévő kis húrocska hajlásszógének kiszámításával kezdődik, mindjárt fokokba átszámolva (erre a fotel megfelelő elfordításához van szükség). Emlékezzünk azonban, hogy az arcus tangens függvény igen sokértékű, s a programnyelvekbe beépített megfelelő függvények ennek csak a "főágával" (azaz szögértékben kifejezve rendszerint csak -90˚ és +90˚ között) dolgoznak. Esetünkben viszont a tárgyalóasztalt körbe kell rakni fotelekkel, így a teljes 360˚ -os szögtartományra szükség van. Ezt oldja meg az utasításmag második sora. Programunk egyben arra is példa, hogy feltételes utasítások (és a velük sok szempontból rokon ciklusszerkezetek) tetszés szerint egymásba építhetők, de a belső szerkezet a külső határait persze nem lépheti át. A helyes elfordítási szög kiszámítása után elhelyezhetjük a soronlévő fotelt, és a következő fotel elhelyezéséhez átállíthatjuk az ezt vezérlő arcl változót.

2.2 Kísérletek, tanulságok. A közelítés pontossága, a gondolkodás ökonómiája.

A jelen feladat elején álló ábra úgy készült, hogy a megfelelő cellákban látható számértékek mellett lefuttattuk a rendez makrót, majd a középponti koordinátákat (G4:G5 cellák) megváltoztatva lefuttatttuk a targyalo makrót. A kétféle szempontú elrendezés közötti kűlönbség szemléletesen jelentkezik.

A rendez makró esetében olyan számítási módszereket alkalmaztunk, amelyeket többnyire közelítő módszereknek neveznek (az érintő hajlásszögét a megfelelő kis húr hajlásszögével, az ellipszisgörbe ívhosszát a beleírt igen sok oldalú húrpoligon oldalhosszainak összegével helyettesítettűk). A számítógépes munkánál igen gyakran fordul elő olyan helyzet, hogy kiszámíttatunk a géppel valamit, de ez nem egészen az amit "tulajdonképpen szeretnénk". Esetünkben "tulajdonképpen" az ellipszis "valódi" ívhosszaival szerettünk volna dolgozni, s e helyett használtuk a húrpoligont. De hát ez az eredeti, "naív" szándékunk eleve reménytelen volt, hiszen már a körív "valódi" hosszát sem tudhatjuk pontosan, mivel mindig ott van benne a p, ez a nem periodikus végtelen tört! A számítógépes módszerek csak ráirányítják a figyelmet az emberi megismerés olyan korlátaira, vagy inkább sajátosságaira, amelyek korábban is jelen voltak, csak legtöbbűnkben nem tudatosodtak. A jelen bekezdés elsö mondatában a "közelítő módszer" kifejezést azért használtuk bizonyos fenntartással, mert igazából nincs mivel szembeállítani. Pontos gondolatmenet létezik az absztrakt matematikában, de amint számszerűsíteni kell valamit, akár papirra számjegyekkel leírva, akár a számítógép véges sok bit-ből álló regisztereivel kifejezve, az igazi pontosság az egész számok (vagy, ami ugyanaz, a véges törtek) körére korlátozódik.

Jóllehet az abszolút pontosság olyan elméleti fogalom, amely a konkrét számításokban többnyire nem valósul meg, az eredmények rendszerint mégis jól használhatóak. Kisérletezzünk a felosztás finomságát megszabó nf érték változtatásával. A jelen fejezet elején álló ábrán egy kis táblázat mutatja, milyen eredményt kapunk a teljes ellipszis kerületének értékére attól függően, hogy a közelítő húrpoligont fokonkénti felosztással, vagy még finomabban, egy fokot még tovább nf részre osztva képezzük. Láthatjuk, hogy akár tizedfokokkal dolgozunk, akár ötvened fokokkal, az eredmény hat értékes jegyre megegyezik. Már a fokonkénti számítás is 1 miliméternél kevésbé tér el a legfinomabb felosztással adódó értéktől. Az ilyen egyszerű összevetések is érzékeltetik az eredmény műszaki szempontból való használhatóságát.

Természetesen az eredmények helyességének, pontosságának a kérdését ennél szabatosabb matematikai módszerekkel is lehet és szükséges vizsgálni. Törekedjünk az eredmény olyan becslésére, amely két számot ad meg, s a helyes, pontos eredmény bizonyíthatóan e két érték közé esik. Esetünkben például biztos, hogy a negyedellipszis ívhossza kisebb mint a két féltengely összege, és nagyobb, mint a két féltengely alkotta derékszögű háromszőg átfogója.Ha ezt az ellenőrző becslést a tárgyalt feladatra alkalmazzuk, két dolgot kell figyelembe venni:

1. feladatunk az ülőhelyek kiosztása volt, így a program az ülőhelyek középpontjain átmenő ellipszissel dolgozik, s a kiszámított kerületérték is erre vonatkozik (nem pedig az asztal kerületére);

2. a mindenkori képenyőmérethez való igazodás érdekében a rajz nagyságát egy m tényezővel változtathatóvá tettük, ami a példa esetén m = 0.7 –re volt beállítva.

Mindezt számításba véve annak az ellipszisnek az a’ és b’ féltengelyei, amire a kiszámított (közelítő) kerületérték vonatkozik

a’ = (a / 2 + 0.55 * c) * m = 87.325 és b’ = (b / 2 + 0.55 * c)* m = 69.825.

Ezekkel számolva a két féltengely összegének négyszerese adja a kerület biztos felső korlátját kf = 628.6, és a két féltengely, mint befogók által alkotott derákszögű háromszög átfogójának négyszerese ka = 447.235 pedig az alsó korlátját. Láthatjuk, hogy

ka < k=495.23 < kf ,

azaz a nyert számérték a durva, de biztos korlátok közé esik. Az ilyesfajta ellenőrzés a közelítő számítás rendszerében, vagy programjában lévő esetleges hibák felderítésére hasznos, az elvileg helyes eljárás közelítésének jóságát pedig a korábban már vizsgált, különböző számítási finomságú futtatások eredményeinek egybevetésével vizsgálhatjuk. A kapott eredmény realitásának gondos mérlegeléséről soha sem szabad megfeledkezni. Már viszonylag egyszerű feladatoknál (pl. görbe felületek felszínszámításánál) is előfordulhat, hogy első látásra kézenfekvőnek tűnő véges elem felosztás teljesen téves számeredményre vezet. Az építészmérnöki alkalmazásoknál az eredmények helyességéért végeredményben mindig az építészmérnök a felelős.